题目内容
17.确定f(x)=x3-3x在哪个区间上是增函数,在哪个区间上是减函数.分析 先求函数的导函数,再解不等式f′(x)>0和f′(x)<0得函数的单调区间.
解答 解:∵f′(x)=3x2-3=3(x+1)(x-1),
令f′(x)>0,解得:x>1或x<-1,令f′(x)<0,解得:-1<x<1,
∴函数f(x)=x3-3x在(-∞,-1)是增函数,在(-1,1)上是减函数,在(1,+∞)是增函数.
点评 要先确定出导函数等于零的实数x的值,再讨论出函数的单调区间,体现了导数的工具作用.

练习册系列答案
相关题目
8.在数列{an}中,a1=3,an=$\sqrt{{a}_{n-1}+2}$,则( )
| A. | 数列{an}单调递减 | B. | 数列{an}单调递增 | ||
| C. | 数列{an}先递减后递增 | D. | 数列{an}先递增后递减 |
12.化简$\frac{1}{\sqrt{1+ta{n}^{2}160°}}$的结果为( )
| A. | -cos160° | B. | cos160° | C. | $\frac{1}{cos160°}$ | D. | $\frac{1}{-cos160°}$ |
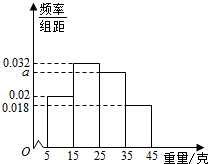 一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25](25,35],(35,45],由此得到样本的重量频率分布直方图,如图.
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25](25,35],(35,45],由此得到样本的重量频率分布直方图,如图.