题目内容
8.已知正方形ABCD的边长为1,点E,F分别为BC、CD的中点,则$\overrightarrow{AE}$•$\overrightarrow{BD}$=-$\frac{1}{2}$.分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AE}$,$\overrightarrow{BD}$在进行数量级运算.
解答 解:∵AB⊥AD,∴$\overrightarrow{AB}•\overrightarrow{AD}=0$.
∵$\overrightarrow{AE}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$,
∴$\overrightarrow{AE}•\overrightarrow{BD}$=($\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$)•($\overrightarrow{AD}-\overrightarrow{AB}$)=-${\overrightarrow{AB}}^{2}$+$\frac{1}{2}{\overrightarrow{AD}}^{2}$=-1+$\frac{1}{2}$=-$\frac{1}{2}$.
故答案为-$\frac{1}{2}$.
点评 本题考查了平面向量的数量级运算,属于基础题.

练习册系列答案
相关题目
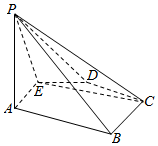 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.