题目内容
6．命题“$?{x_0}∈R，使得x_0^2≥0$”的命题的否定为?x∈R，使得x2＜0．分析 直接利用特称命题的否定是全称命题写出结果即可．
解答 解：因为特称命题的否定是全称命题，所以命题的否定为：?x∈R，使得x2＜0．．
故答案为：?x∈R，使得x2＜0．
点评 本题考查命题的否定特称命题与全称命题的关系，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
17．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（ ）
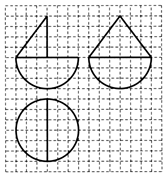
| A． | 24π | B． | 30π | C． | 42π | D． | 60π |
如图所示函数图象，
1．已知△ABC的顶点B，C在椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$上，顶点A是椭圆的一个焦点，且椭圆的另一个焦点在BC上，则△ABC的周长是（ ）
| A． | 8 | B． | 8$\sqrt{3}$ | C． | 16 | D． | 24 |
11．与球心距离为1的截球平面，所得的截面圆的面积为2π，则球的体积为（ ）
| A． | 8$\sqrt{3}$π | B． | 4$\sqrt{3}$π | C． | 4π | D． | 8π |
15．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 4 | D． | 8 |
16．若复数z=$\frac{2}{1+i}$+（1-i）2，则|z|等于（ ）
| A． | $\sqrt{10}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{5}$ |