题目内容
7.已知函数f(x)=$\frac{1}{a}$-$\frac{1}{x}$ (a>0,x>0).(1)用定义法证明:f(x)在(0,+∞)上是增函数;
(2)若f(x)≤2x在(0,+∞)上恒成立,求a的取值范围;
(3)若f(x)在[m,n]上的值域是[m,n](m≠n),求a的取值范围.
分析 (1)由增函数的定义直接证明即可得出;
(2)f(x)≤2x在(0,+∞)上恒成立,可转化为2ax2-x+a≥0在(0,+∞)上恒成立,由此可得a>0,再判断出函数f(x)=2ax2-x+a在(0,+∞)上的最小值,令其大于等于0,解此不等式即可得出;
(3)由题设,本题可转化为 $\frac{1}{a}$-$\frac{1}{x}$=x有两个根,即ax2-x+a=0有两个不等根,由此利用判别式得到a的不等式,解之即可.
解答 解:(1)任取x1,x2∈(0,+∞),且x1<x2,则
f(x1)-f(x2)=$\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{1}}$=$\frac{{{x}_{1}-x}_{2}}{{{x}_{1}x}_{2}}$,
∵x1,x2∈(0,+∞),且x1<x2,
∴x1x2>0,x1-x2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(0,+∞)上是增函数;
(2)f(x)≤2x在(0,+∞)上恒成立,即$\frac{1}{a}$-$\frac{1}{x}$≤2x在(0,+∞)上恒成立,
即2ax2-x+a≥0在(0,+∞)上恒成立,可得a>0,
所以其对称轴为x=$\frac{1}{4a}$>0,
由相应二次函数的性质得x=$\frac{1}{4a}$时,2ax2-x+a≥0成立即可,
∴2a( $\frac{1}{4a}$)2-$\frac{1}{4a}$+a≥0,解得a≥$\frac{\sqrt{2}}{4}$或a≤-$\frac{\sqrt{2}}{4}$(舍),
故a的取值范围是a≥$\frac{\sqrt{2}}{4}$;
(3)由(1),f(x)在(0,+∞)上是增函数,又f(x)在[m,n]上的值域是[m,n](m≠n),
∴$\left\{\begin{array}{l}{\frac{1}{a}-\frac{1}{m}=m}\\{\frac{1}{a}-\frac{1}{n}=n}\end{array}\right.$,即 $\frac{1}{a}$-$\frac{1}{x}$=x有两个根,即ax2-x+a=0有两个不等根,
∴△=1-4a2>0,解得-$\frac{1}{2}$<a<$\frac{1}{2}$,又a>0,
实数a的取值范围为0<a<$\frac{1}{2}$.
点评 本题考查函数恒成立问题的一般转化方法,函数单调性的证明,二次函数的性质,转化的思想,最值的应用,综合性强.

| A. | (1)(3) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
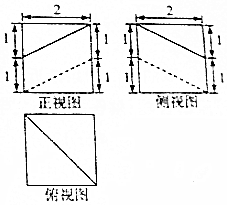 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 7 |
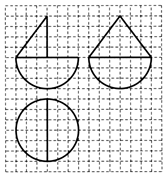
| A. | 24π | B. | 30π | C. | 42π | D. | 60π |