题目内容
如图(1),在边长为2的正方形ABCD中,E是边AB的中点.将△ADE沿DE折起使得平面ADE⊥平面BCDE,如图(2),F是折叠后AC的中点.
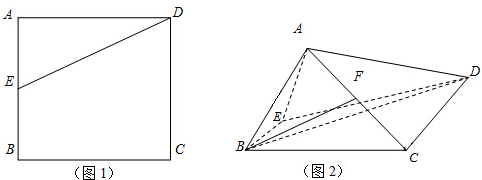
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)求二面角E-AB-D的平面角的余弦值.

(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)求二面角E-AB-D的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ) 取AD中点G,连结EG,FG,由已知得四边形EBFG是平行四边形,从而BF∥EG,由此能证明EG∥平面ADE.
(Ⅱ) 以E为坐标原点,建立空间直角坐标系,分别求出平面EAB的法向量和平面ABD的法向量,由此能求出二面角E-AB-D的平面角的余弦值.
(Ⅱ) 以E为坐标原点,建立空间直角坐标系,分别求出平面EAB的法向量和平面ABD的法向量,由此能求出二面角E-AB-D的平面角的余弦值.
解答:
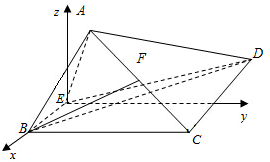 解:(Ⅰ) 证明:取AD中点G,连结EG,FG,
解:(Ⅰ) 证明:取AD中点G,连结EG,FG,
∵F为AC中点,∴FG
CD,BE
CD,
∴FG
BE,
∴四边形EBFG是平行四边形…(3分)
∴BF∥EG,又BF?平面ADE,EG?平面ADE,
∴BF∥平面ADE.…(7分)
(Ⅱ) 如图示以E为坐标原点,
建立空间直角坐标系
则由已知得A(-
,
,
),
B(1,0,0),D(-1,2,0)
设平面EAB的法向量为
=(x1,y1,z1)
则
⇒
解得一个法向量为
=(0,
,-1)…(10分)
设平面ABD的法向量为
=(x2,y2,z2)
则
⇒
解得一个法向量为
=(
,
,2)…(13分)
∵cos<
,
>=
=
,
∴二面角E-AB-D的平面角的余弦值
.…(15分)
 解:(Ⅰ) 证明:取AD中点G,连结EG,FG,
解:(Ⅰ) 证明:取AD中点G,连结EG,FG,∵F为AC中点,∴FG
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
∴FG
| ||
. |
∴四边形EBFG是平行四边形…(3分)
∴BF∥EG,又BF?平面ADE,EG?平面ADE,
∴BF∥平面ADE.…(7分)
(Ⅱ) 如图示以E为坐标原点,
建立空间直角坐标系
则由已知得A(-
| 1 |
| 5 |
| 2 |
| 5 |
| 2 | ||
|
B(1,0,0),D(-1,2,0)
设平面EAB的法向量为
| n1 |
则
|
|
解得一个法向量为
| n1 |
| 5 |
设平面ABD的法向量为
| n2 |
则
|
|
解得一个法向量为
| n2 |
| 5 |
| 5 |
∵cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 14 |
∴二面角E-AB-D的平面角的余弦值
| ||
| 14 |
点评:本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
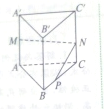 如图,在直棱柱ABC-A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为
如图,在直棱柱ABC-A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为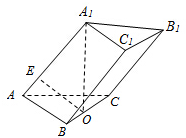 在三棱柱ABC-A1B1C1中,已知AA1=8,AC=AB=5,BC=6,点A1在底面ABC的射影是线段BC的中点O,在侧棱AA1上存在一点E,且OE⊥B1C.
在三棱柱ABC-A1B1C1中,已知AA1=8,AC=AB=5,BC=6,点A1在底面ABC的射影是线段BC的中点O,在侧棱AA1上存在一点E,且OE⊥B1C.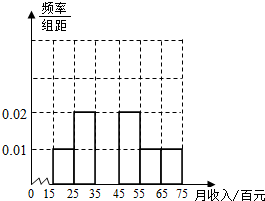 为了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,做出了他们的月收入(单位:百元,范围:[15,75])的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
为了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,做出了他们的月收入(单位:百元,范围:[15,75])的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表: