题目内容
11.已知数列{an},Sn是其前n项和,满足${S_n}+{S_{n+1}}=2{n^2}+b$,a1=a.(1)若a=b=1,
(i)求出a2,a3的值;
(ii)求{an}的通项公式.
(2)是否存在一个各项均为正数的等比数列{bn},存在一个数列{an}满足an=lnbn,如果存在,求出{an}和{bn}的通项公式,如果不存在,说明理由.
分析 (1)(i)由已知数列递推式结合a=b=1求得a2,a3的值;
(ii)把已知数列递推式变形为$2{S}_{n}+{a}_{n+1}=2{n}^{2}+1$,当n≥2时,$2{S_{n-1}}+{a_n}=2{({n-1})^2}+1$,两式作差可得an+an+1=4n-2,进一步得到an+2-an=4.然后分n为偶数和n为奇数求得数列通项公式;
(2)假设存在这样的{an}和{bn},结合$2{S}_{n}+{a}_{n+1}=2{n}^{2}+b$,a1=a,求得a2,a3,a4,由ea,e2+b-2a,e2a+4-b,e6+2b-a成等比,列式解得a=0,b=0.然后验证a=0,b=0时,数列{bn}为等比数列,并进一步求得数列{bn}的通项公式.
解答 解:(1)(i)由题可得${a_1}+{a_1}+{a_2}=2×{1^2}+1$,∴a2=1,
${a_1}+{a_2}+{a_1}+{a_2}+{a_3}=2×{2^2}+1$,∴a3=5;
(ii)由题意,即$2{S}_{n}+{a}_{n+1}=2{n}^{2}+1$,
当n≥2时,$2{S_{n-1}}+{a_n}=2{({n-1})^2}+1$,作差可得2an+an+1-an=4n-2,
即an+an+1=4n-2,∴an+1+an+2=4(n+1)-2.
作差可得an+2-an=4.
当n为偶数时,${a_n}={a_2}+4×({\frac{n-2}{2}+1-1})=2n-3$;
当为奇数时,${a_n}={a_3}+4×({\frac{n-3}{2}+1-1})=2n-1$.
经检验,n=1也符合.
综上,${a_n}=\left\{{\begin{array}{l}{2n-1,n=2k-1}\\{2n-3,n=2k}\end{array}}\right.,k∈{N^*}$;
(2)假设存在这样的{an}和{bn},那么$2{S}_{n}+{a}_{n+1}=2{n}^{2}+b$,
∵a1=a,2a1+a2=2+b,∴a2=2+b-2a,S2=2+b-a,
∴2S2+a3=8+b,a3=2a+4-b,S3=a+6,
∴2S3+a4=18+b,∴a4=6+2b-a,
∴ea,e2+b-2a,e2a+4-b,e6+2b-a成等比,可得
ea•e2a+4-b=(e2+b-2a)2,e2+b-2a•e6+2b-a=(e2a+4-b)2.
即$\left\{\begin{array}{l}{a+2a+4-b=2(2+b-2a)}\\{2+b-2a+6+2b-a=2(2a+4-b)}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=0}\\{b=0}\end{array}\right.$.
下面检验当a=0,b=0时,数列{bn}为等比数列.
由题得a1=0,${S_n}+{S_{n+1}}=2{n^2}$,
当n≥2时,
∴${S_{n-1}}+{S_n}=2{({n-1})^2}$,
作差可得an+an+1=4n-2,
a2=2-2S1=2,显然n=1时也符合上式.
∴an+2+an+1=4n+2,可得an+2-an=4.
当n为偶数时,${a_n}={a_2}+({\frac{n-2}{2}+1-1})×4=2+2n-4=2n-2$,
当n为奇数时,${a_n}={a_1}+({\frac{n-1}{2}+1-1})×4=2n-2$.
∴an=2n-2
那么${b_n}={e^{a_n}}={e^{2n-2}}$,$\frac{{{b_{n+1}}}}{b_n}=\frac{{{e^{2n}}}}{{{e^{2n-2}}}}={e^2}$是等比数列,
∴存在这样的等比数列{bn}和数列{an},使得等式成立,
${a}_{n}=2n-2,{b}_{n}={e}^{2n-2}$.
点评 本题考查数列递推式,考查了等差数列和等比数列的通项公式,考查数列的函数特性,考查逻辑思维能力和推理论证能力,属难题.

| A. | ?x∈(0,$\frac{π}{2}$),使得cos x>x | B. | ?x∈(0,$\frac{π}{2}$),使得cos x≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cos x<x | D. | ?x∈(0,$\frac{π}{2}$),使得cos x<x |
| A. | a+1>b | B. | 2a>2b | C. | a2>b2 | D. | lga>lgb |
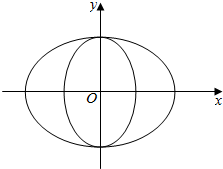 如图,曲线Γ由两个椭圆T1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$和椭圆T2:$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1({b>c>0})$组成,当a,b,c成等比数列时,称曲线Γ为“猫眼曲线”.
如图,曲线Γ由两个椭圆T1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$和椭圆T2:$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1({b>c>0})$组成,当a,b,c成等比数列时,称曲线Γ为“猫眼曲线”. 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.