题目内容
已知数列{an}满足:a1=1,a2=2,且an+2=(2+cosnπ)(an-1)+3,n∈N*.
(1)求通项公式an;
(2)求数列的前n项的和Sn.
(1)求通项公式an;
(2)求数列的前n项的和Sn.
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)讨论n的奇偶性,即可求通项公式an;
(2)根据等差数列和等比数列的前n项和公式,即可求数列的前n项的和Sn.
(2)根据等差数列和等比数列的前n项和公式,即可求数列的前n项的和Sn.
解答:
解:(1)当n是奇数时,cosnπ=-1,
所以an+2=an+2,所以a1,a3,a5,…,a2n-1,…是首项为a1=1,公差为2的等差数列,因此a2n-1=2n-1.
当n为偶数时,cosnπ=1,所以an+2=3an,所以a2,a4,a6,…,a2n,…是首项为a2=2,公比为3的等比数列,因此a2n=2×3n-1.
综上an=
.
(2)由(1)得S2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)=3n+n2-1,
S2n-1=S2n-a2n=3n-1+n2-1,
所以Sn=
.
所以an+2=an+2,所以a1,a3,a5,…,a2n-1,…是首项为a1=1,公差为2的等差数列,因此a2n-1=2n-1.
当n为偶数时,cosnπ=1,所以an+2=3an,所以a2,a4,a6,…,a2n,…是首项为a2=2,公比为3的等比数列,因此a2n=2×3n-1.
综上an=
|
(2)由(1)得S2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)=3n+n2-1,
S2n-1=S2n-a2n=3n-1+n2-1,
所以Sn=
|
点评:本题主要考查数列的通项公式的求解以及数列求和的计算,考查学生的运算能力,本题注意要注意对n进行分类讨论.

练习册系列答案
相关题目
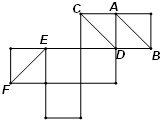 如图是一个正方体纸展开图,如果将它还原成正方体,那么直线AB,CD,EF在原正方体的位置关系是( )
如图是一个正方体纸展开图,如果将它还原成正方体,那么直线AB,CD,EF在原正方体的位置关系是( )| A、AB∥CD,EF⊥CD |
| B、AB与CD异面成角60°,CD与EF相交成角60° |
| C、AB∥CD,CD与EF相交成角60° |
| D、EF⊥CD,AB与CD异面成角60° |
函数f(x)=lg
的图象( )
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
 在平面直角坐标系xOy中,椭圆E:
在平面直角坐标系xOy中,椭圆E: