题目内容
6.{an}数列的前n项和Sn符合Sn=k(2n-1)且a3=8,(1)求{an}通项公式;
(2)求{nan}的前n项和Tn.
分析 (1)由已知取得k值,得到首项与前n项和,再由an=Sn-Sn-1(n≥2)求得数列通项公式;
(2)利用错位相减法求{nan}的前n项和Tn.
解答 解:(1)由Sn=k(2n-1),得a1=S1=k,
a3=S3-S2=7k-3k=4k=8,
∴k=2.
则Sn=k(2n-1)=2n+1-2.
∴当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=({2}^{n+1}-2)-({2}^{n}-2)={2}^{n}$.
a1=2适合上式,
∴${a}_{n}={2}^{n}$;
(2)nan=n•2n,
∴${T}_{n}=1•{2}^{1}+2•{2}^{2}+3•{2}^{3}+…+n•{2}^{n}$,
则$2{T}_{n}=1•{2}^{2}+2•{2}^{3}+…+n•{2}^{n+1}$,
两式作差得:$-{T}_{n}=2+{2}^{2}+…+{2}^{n}-n•{2}^{n+1}$=$\frac{2(1-{2}^{n})}{1-2}-n•{2}^{n+1}={2}^{n+1}-2-n•{2}^{n+1}$.
∴${T}_{n}=(n-1)•{2}^{n+1}+2$.
点评 本题考查数列递推式,考查由数列的前n项和求通项,训练了错位相减法求数列的前n项和,是中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16.极坐标方程ρ=2cosθ-4sinθ对应的直角坐标方程为( )
| A. | (x-1)2+(y+2)2=5 | B. | (x-1)2+(y-2)2=5 | C. | (x-2)2+(y-1)2=5 | D. | (x+1)2+(y+2)2=5 |
17.设A、B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧,在河岸边选定一点C,测出AC的距离是100m,∠BAC=60°,∠ACB=30°,则A、B两点的距离为( )
| A. | 40 m | B. | 50 m | C. | 60 m | D. | 70 m |
14.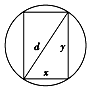 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )| A. | $\sqrt{3}$d,$\frac{\sqrt{3}}{3}$d | B. | $\frac{\sqrt{3}}{3}$d,$\frac{\sqrt{6}}{3}$d | C. | $\frac{\sqrt{6}}{3}$d,$\frac{\sqrt{3}}{3}$d | D. | $\frac{\sqrt{6}}{3}$d,$\sqrt{3}$d |
18.设i为虚数单位,复数z1=1-i,z2=2i-1,则复数z1•z2在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.y=sin2x的图象向左平移$\frac{π}{4}$个单位,再向上平移1个单位,所得图象的函数解析式是( )
| A. | y=2cos2x | B. | y=2sin2x | C. | y=1+sin(2x+$\frac{π}{4}$) | D. | y=cos2x |
16.已知等差数列$\{a_n^{\;}\}$的前n项和为Sn,若a2+a8+a11=30,求S13=( )
| A. | 130 | B. | 65 | C. | 70 | D. | 140 |