Question

已知函数f（x）=

3

sin

x

2

cos

x

2

+cos²

x

2

+m的图象过点（

5π

6

，0）．
（Ⅰ）求实数m值以及函数f（x）的单调递增区间；
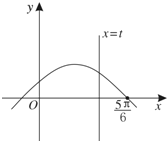
（Ⅱ）设y=f（x）的图象与x轴、y轴及直线x=t（0＜t＜

2π

3

）所围成的曲边四边形面积为S，求S关于t的函数S（t）的解析式．

Answer 1

考点：三角函数中的恒等变换应用,定积分在求面积中的应用

专题：计算题,三角函数的图像与性质

分析：（Ⅰ）利用二倍角的正弦和余弦公式降幂，化为y=sin(x+

π

6

)+

1

2

+m的形式，把点（

5π

6

，0）代入函数解析式求得m的值，再代入函数解析式后利用复合函数的单调性求得函数f（x）的单调递增区间；
（Ⅱ）对（Ⅰ）中所求函数f（x）求0到t上的积分，即求被积函数f（x）的原函数，代入积分上限和下限后作差得答案．

解答： 解：（I）f（x）=

3

sin

x

2

cos

x

2

+cos²

x

2

+m
=

3

2

sinx+

1

2

cosx+

1

2

+m
=sin(x+

π

6

)+

1

2

+m．
∵f（x）的图象过点（

5π

6

，0），
∴sin(

5π

6

+

π

6

)+

1

2

+m=0，解得m=-

1

2

．
∴f（x）=sin(x+

π

6

)，
由-

π

2

+2kπ≤x+

π

6

≤

π

2

+2kπ，得-

2π

3

+2kπ≤x≤

π

3

+2kπ，k∈Z．
故f（x）的单调递增区间是[-

2π

3

+2kπ，

π

3

+2kπ]，k∈Z；
（Ⅱ）由（I）得，f（x）=

3

2

sinx+

1

2

cosx．
∴S

=∫

t 0

(

3

2

sinx+

1

2

cosx)dx=(-

3

2

cosx+

1

2

sinx)

|

t 0

=(-

3

2

cost+

1

2

sint)-(-

3

2

cos0+

1

2

sin0)=sin(t-

π

3

)+

3

2

．
∴S(t)=sin(t-

π

3

)+

3

2

（0＜t＜

2π

3

）．

点评：本题主要考查二倍角公式、两角和与差的三角函数公式、三角函数的图象与性质及定积分等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想、函数与方程思想，是中档题．