题目内容
（1）求证：a logaN=N（a＞0，且a≠1）
（2）用（1）的结论求下列式子的值．（其中③需详细写出解答过程）
①2 log264②3 2log39③2 log4(2-
)2+3 log9(2+
)2．
（2）用（1）的结论求下列式子的值．（其中③需详细写出解答过程）
①2 log264②3 2log39③2 log4(2-
| 3 |
| 3 |
考点：对数的运算性质
专题：计算题,函数的性质及应用
分析：（1）由对数的定义，可知，ab=N?logaN=b，运用代入法，即可得证；
（2）运用（1）的结论，以及对数的运算法则，即可求得．
（2）运用（1）的结论，以及对数的运算法则，即可求得．
解答：
（1）证明：由对数的定义，可知，ab=N?logaN=b，
将b=logaN，代入ab=N，即得alogaN=N；
（2）解：①2log264=64；
②32log39=3log381=81；
③2 log4(2-
)2+3 log9(2+
)2=22log4(2-
)+32log9(2+
)
=4log4(2-
)+9log9(2+
)=2-
+2+
=4．
将b=logaN，代入ab=N，即得alogaN=N；
（2）解：①2log264=64；
②32log39=3log381=81；
③2 log4(2-
| 3 |
| 3 |
| 3 |
| 3 |
=4log4(2-
| 3 |
| 3 |
| 3 |
| 3 |
点评：本题考查对数的定义和对数恒等式的运用，考查对数的运算法则，考查运算能力，属于基础题．
练习册系列答案
相关题目
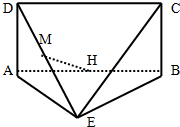已知平面ABCD⊥平面ABE，四边形ABCD是矩形，AD=AE=BE=2，M、H分别是DE、AB的中点，主（正）视图方向垂直平面ABCD时，左（侧）视图的面积为