题目内容
17．双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的左焦点与右顶点之间的距离等于（ ）| A． | 6 | B． | 8 | C． | 9 | D． | 10 |
分析 根据题意，由双曲线的标准方程可得a2、b2的值，计算可得其左焦点和右顶点的坐标，计算可得左焦点与右顶点之间的距离，即可得答案．
解答 解：根据题意，双曲线的标准方程为：$\frac{x^2}{9}-\frac{y^2}{16}=1$，
其中a2=9，b2=16，则c=$\sqrt{9+16}$=5，
则其左焦点坐标为（-5，0），右顶点坐标为（3，0）；
故左焦点与右顶点之间的距离8；
故选：B．
点评 本题考查双曲线的标准方程的应用，关键是利用双曲线的标准方程求出焦点坐标以及顶点坐标．
练习册系列答案
相关题目
12．
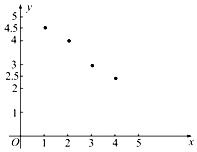如表是某厂1～4月份用水量（单位：百吨）的一组数据．由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a，则a=（ ）
如表是某厂1～4月份用水量（单位：百吨）的一组数据．由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a，则a=（ ）| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A． | 10.5 | B． | 5.15 | C． | 5.2 | D． | 5.25 |
9．已知在极坐标系中，点A（2，$\frac{π}{2}$），B（$\sqrt{2}$，$\frac{3π}{4}$），O（0，0），则△ABO为（ ）
| A． | 正三角形 | B． | 直角三角形 | C． | 等腰锐角三角形 | D． | 等腰直角三角形 |
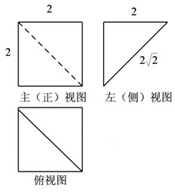
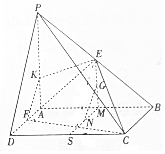在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为矩形，点E，F，M，S分别为棱PB，AD，AB，CD的中点，G为线段EM的中点，且PA=AB=2AD=4，N为SM上一点，且NG∥平面CEF．