题目内容
12．已知${（{1+x}）^{10}}={a_0}+{a_1}（{1-x}）+{a_2}{（{1-x}）^2}+L+{a_{10}}{（{1-x}）^{10}}$，则a8等于（ ）| A． | -5 | B． | 5 | C． | 90 | D． | 180 |
分析 将1+x写成2-（1-x），利用二项展开式的通项公式求出通项，令1-x的指数为8，即可求出a8
解答 解：∵（1+x）10=[2-（1-x）]10，
∴其展开式的通项为：
Tr+1=（-1）r210-rC10r（1-x）r，
令r=8，得a8=4C108=180．
故选：D．
点评 本题考查了利用二次展开式的通项公式求展开式的特定项问题，关键是将底数改写成右边的底数形式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，曲线Γ由曲线C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0，y≤0）和曲线C2：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0，y＞0）组成，其中点F1，
20．定义在R上的偶函数f（x）满足f（x）+f（x-1）=0，且在[-5，-4]上是增函数，A，B是锐角三角形的两个内角，则（ ）
| A． | f（sinA）＞f（cosB） | B． | f（sinA）＜f（cosB） | C． | f（sinA）＞f（sinB） | D． | f（cosA）＞f（cosB） |
17．$k=±\frac{{\sqrt{5}}}{2}$是直线y=kx-1与曲线x2-y2=4仅有一个公共点的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
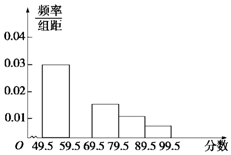在长丰中学举行的电脑知识竞赛中，将九年级两个班参赛的学生成绩（得分均为整数）进行整理后分成五组，绘制如图所示的频率分布直方图．已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30，0.15，0.10，0.05，第二小组的频数是40．