题目内容
6.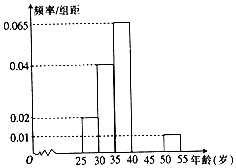 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.(1)求第五组的频率并估计200名志愿者中年龄在40岁以上(含40岁)的人数;
(2)若从年龄位于第四组和第六组的志愿者中随机抽取两名,记他们的年龄分别为x,y,事件E={|x-y|≤5},求P(E).
分析 (1)先求出第四组的频率,从而能求出第五组的频率,由直方图求出后三组频率,由此能求出200名志愿者中年龄在40岁以上(含40岁)的人数.
(2)第四组[40,45)的人数为4人,设为a,b,c,d;第六组[50,55]的人数为2人,设为A,B.利用列举法能求出事件E包含的基本事件个数.
解答 解:(1)第四组的频率为$\frac{4}{40}=0.1$,
所以第五组的频率为1-0.1-5×(0.02+0.04+0.065+0.01)=0.225,
由直方图得后三组频率为0.1+0.225+0.01×5=0.375.
所以200名志愿者中年龄在40岁以上(含40岁)的人数约为0.375×200=75人.
(2)第四组[40,45)的人数为4人,
设为a,b,c,d;
第六组[50,55]的人数为2人,设为A,B.
则有ab,ac,ad,bc,bd,cd,aA,bA,cA,dA,aB,bB,cB,dB,AB共15种情况,
因事件E={|x-y|≤5}发生当且仅当随机抽取的两名志愿者在同一组,
所以事件E包含的基本事件为ab,ac,ad,bc,bd,cd,AB共 7 种情况,
故$P(E)=\frac{7}{15}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查学生分析解决问题的能力,考查数据处理能力、运算求解能力,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.某篮球运动员在最近5场比赛中所得分数分别为12,a,8,15,23,其中a>0,若该运动员在这5场比赛中得分的中位数为12,则得分的平均数不可能为( )
| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | $\frac{71}{5}$ | D. | 14 |
18.设正三棱锥A-BCD内接于球O,BC=1,E为AB的中点,AC⊥DE,则球的半径为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.