题目内容
16.已知直线l与抛物线y2=2px(p>0)交于A,B两点,D为坐标原点,且OA⊥OB,OD⊥AB于点D,点D的坐标为(1,2),则p=$\frac{5}{2}$.分析 求得OD的斜率,即可求得直线AB的方程,设出A,B的坐标,由OA⊥OB得到A,B横纵坐标的关系,联立直线方程和抛物线方程,化为关于y的方程后利用根与系数的关系求解.
解答 解:∵点D的坐标为(1,2),则kOD=2,
又OD⊥AB,且AB过D(1,2),
则直线AB的方程:y-2=-$\frac{1}{2}$(x-1),整理得:2y+x-5=0;
设点A的坐标(x1,y1),点B的坐标(x2,y2),
由OA⊥OB,则$\overrightarrow{OA}$+$\overrightarrow{OB}$=0,即x1x2+y1y2=0,
则AB的直线方程为x=5-2y,
∴y1y2-2(y1+y2)+5=0,①
则$\left\{\begin{array}{l}{x=5-2y}\\{{y}^{2}=2px}\end{array}\right.$,消去x得:y2-4py-10p=0,
y1+y2=4p,y1y2=-10p,②
把②代入解得p=$\frac{5}{2}$,
∴p的值$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查直线的方程,直线与抛物线的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
6.设i是虚数单位,复数z满足z•(1+2i)2=3+4i,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.椭圆my2+x2=1的一个顶点在抛物线$y=\frac{1}{2}{x^2}$的准线上,则椭圆的离心率( )
| A. | $\frac{{\sqrt{63}}}{8}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 4 | D. | $\frac{{\sqrt{5}}}{2}$ |
4.若两个不同平面α、β的法向量分别为$\overrightarrow{u}$=(1,2,-1),$\overrightarrow{v}$=(-2,2,2),则( )
| A. | α、β相交但不垂直 | B. | α⊥β | C. | α∥β | D. | 以上均不正确 |
11. 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )| A. | -$\frac{\sqrt{65}}{13}$ | B. | $\frac{\sqrt{65}}{13}$ | C. | -$\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{2}}{10}$ |
8.函数 f ( x)=$\frac{x}{lnx}$( x>1)单调递减区间是( )
| A. | (1,+∞) | B. | (1,e2) | C. | (e,+∞) | D. | (1,e) |
5.已知函数f ( x)=ax3+bx2+cx+d 的图象如图所示,则$\frac{b+1}{a+1}$的取值范围是( )
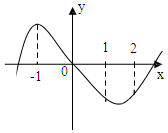

| A. | (-$\frac{3}{2}$,$\frac{1}{2}$ ) | B. | (-$\frac{2}{5}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$) | D. | (-$\frac{3}{2}$,1) |
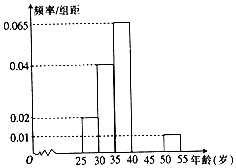 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.