题目内容
1.某篮球运动员在最近5场比赛中所得分数分别为12,a,8,15,23,其中a>0,若该运动员在这5场比赛中得分的中位数为12,则得分的平均数不可能为( )| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | $\frac{71}{5}$ | D. | 14 |
分析 根据中位数为12,得出a≤12,
计算平均数得出结论.
解答 解:若中位数为12,则a≤12,
∴平均分为$\frac{12+a+8+15+23}{5}≤14$=$\frac{70}{5}$,
由选项知平均数不可能为$\frac{71}{5}$.
故选:C.
点评 本题考査了平均数和中位数的应用问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )| A. | -$\frac{\sqrt{65}}{13}$ | B. | $\frac{\sqrt{65}}{13}$ | C. | -$\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{2}}{10}$ |
12.已知数列{an}是等差数列,a1=cot585°,a6=11a1,设Sn为数列{(-1)nan}的前n项和,则S2017=( )
| A. | 3022 | B. | -3022 | C. | 2017 | D. | -2017 |
9.两个变量y与x的回归模型中,分别选择了4个不同模型,它们对应的回归系数r如下,其中变量之间线性相关程度最高的模型是( )
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
16.“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.若一个几何体的三视图都是如图所示的边长为2的正方形,则该几何体的外接球的表面积是( )
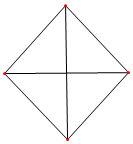

| A. | π | B. | 2π | C. | 4π | D. | 8π |
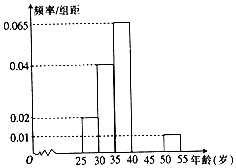 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.