题目内容
设命题p:?x∈[-1,1],x+m>0命题q:方程
-
=1表示双曲线.
(1)写出命题p的否定;
(2)若“p或q”为真,“p且q”为假,求实数m的取值范围.
| x2 |
| m-4 |
| y2 |
| m+2 |
(1)写出命题p的否定;
(2)若“p或q”为真,“p且q”为假,求实数m的取值范围.
考点:复合命题的真假,命题的否定
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:(1)特称命题的否定是特称改全称,否定结论;(2)先解p,q为真时m的取值,然后由“p或q”为真,“p且q”为假,所以p,q一真一假,分类讨论求m的范围.
解答:
解:(1)命题p的否定:?x∈[-1,1],x+m≤0;
(2)由题意可知,p为真时,m>-x≥-1,得m>-1,
q为真时,(m-4)(m+2)>0,解得m>-4或m<-2,
因为“p或q”为真,“p且q”为假,所以p,q一真一假,
当p为真且q为假时,
,解得-1<m≤4;
当p为假且q为真时,
解得m<-2;
综上,实数m的取值范围是m<-2或-1<m≤4.
(2)由题意可知,p为真时,m>-x≥-1,得m>-1,
q为真时,(m-4)(m+2)>0,解得m>-4或m<-2,
因为“p或q”为真,“p且q”为假,所以p,q一真一假,
当p为真且q为假时,
|
当p为假且q为真时,
|
综上,实数m的取值范围是m<-2或-1<m≤4.
点评:本题考查命题的真假判断,注意对联接词的逻辑关系的判断.

练习册系列答案
相关题目
下列说法中,错误的是( )
| A、“荐在实数,使x>1”的否定是“对任意实数x,都有x≤1” |
| B、命题“若m>0,则方程x2+x-m=0有实数根”的否命题是“若m≤0,则方程x2+x-m=0没有实数根” |
| C、若x,y∈R,且x+y<2,则x,y至多有一个大于1 |
| D、设x∈R,则“x<-1”是“2x2-x-3>0”的必要不充分条件 |
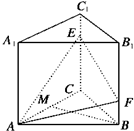 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.