题目内容
设复数a=
,b=
(其中i为虚数单位)
(1)求a2、a3、b2、b3的值;
(2)当n∈N*时,计算an+bn.
1+
| ||
| 2 |
1-
| ||
| 2 |
(1)求a2、a3、b2、b3的值;
(2)当n∈N*时,计算an+bn.
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:(1)利用复数代数形式的运算法则或三角形式的运算法则即可得出;
(2)利用“棣莫弗定理”即可得出.
(2)利用“棣莫弗定理”即可得出.
解答:
解:(1)∵复数a=
,b=
,
∴a=cos
+isin
,b=cos(-
)+isin(-
)=
,
∴a2=cos
+isin
=-
+
i,b2=cos(-
)+isin(-
)=-
-
i.
a3=cosπ+isinπ=-1,b3=cos(-π)+isin(-π)=-1.
(2)由(1)可知:an+bn=(cos
+isin
)n+[cos(-
)+isin(-
)]n
=2cos
+i[sin
+sin(-
)]
=2cos
.
1+
| ||
| 2 |
1-
| ||
| 2 |
∴a=cos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
. |
| a |
∴a2=cos
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
a3=cosπ+isinπ=-1,b3=cos(-π)+isin(-π)=-1.
(2)由(1)可知:an+bn=(cos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=2cos
| nπ |
| 3 |
| nπ |
| 3 |
| nπ |
| 3 |
=2cos
| nπ |
| 3 |
点评:本题考查了复数代数形式的运算法则或“棣莫弗定理”,属于中档题.

练习册系列答案
相关题目
若实数a,b,c满足a2+b2+c2=8,则a+b+c的最大值为( )
| A、9 | ||
B、2
| ||
C、3
| ||
D、2
|
给出下列四个命题,其中假命题是( )
| A、从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样 | ||
| B、样本方差反映了样本数据与样本平均值的偏离程度 | ||
| C、在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 | ||
D、设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(-1<x<0)=
|
已知集合A={x||x+1|<1},B={x|(
)x-2≥0},则A∩∁RB=( )
| 1 |
| 2 |
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
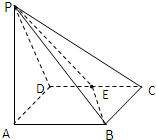 如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°
如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°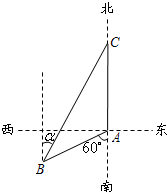 如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?
如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?