题目内容
户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下列联表:
(1)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由;
(2)经进一步调查发现,在喜欢户外运动的10名女性员工中,有6人还喜欢瑜伽.若从喜欢户外运动的10位女性员工中任选2人,求至少有一人喜欢瑜伽的概率
下面的临界值表仅供参考:
(参考公式:K2=
,其中n=a+b+c+d)
| 喜欢户外运动 | 不喜欢户外运动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)经进一步调查发现,在喜欢户外运动的10名女性员工中,有6人还喜欢瑜伽.若从喜欢户外运动的10位女性员工中任选2人,求至少有一人喜欢瑜伽的概率
下面的临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)利用列联表,计算K2,与临界值比较,可得结论;
(2)确定基本事件总数,至少有一人喜欢瑜伽事件总数,即可求出概率
(2)确定基本事件总数,至少有一人喜欢瑜伽事件总数,即可求出概率
解答:
解:(1)K2=
≈8.333>7.879,
∴有99.5%的把握认为喜欢户外运动与性别有关 (5分)
(2)由题意,基本事件的总数为
=45,不满足条件的事件数为
=6,则满足条件的事件数为39,至少有一人喜欢瑜伽的概率p=
=
(13分)
| 50(20×15-10×5)2 |
| 30×20×25×25 |
∴有99.5%的把握认为喜欢户外运动与性别有关 (5分)
(2)由题意,基本事件的总数为
| C | 2 10 |
| C | 2 4 |
| 39 |
| 45 |
| 13 |
| 15 |
点评:本题考查概率与统计知识,考查独立性检验的应用,比较基础.

练习册系列答案
相关题目
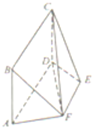 如图,几何体ABCDEF中,四边形ABCD为矩形,且平面ABCD⊥平面ADEF,四边形ADEF为等腰梯形,AD∥EF,AD=2,AB=AF=1,∠DAF=60°.
如图,几何体ABCDEF中,四边形ABCD为矩形,且平面ABCD⊥平面ADEF,四边形ADEF为等腰梯形,AD∥EF,AD=2,AB=AF=1,∠DAF=60°.