题目内容
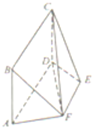 如图,几何体ABCDEF中,四边形ABCD为矩形,且平面ABCD⊥平面ADEF,四边形ADEF为等腰梯形,AD∥EF,AD=2,AB=AF=1,∠DAF=60°.
如图,几何体ABCDEF中,四边形ABCD为矩形,且平面ABCD⊥平面ADEF,四边形ADEF为等腰梯形,AD∥EF,AD=2,AB=AF=1,∠DAF=60°.(Ⅰ)证明:AF⊥平面CDF;
(Ⅱ)求几何体ABCDEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:(Ⅰ)利用线面平行的判定,CD⊥AF,AF⊥DF,∴AF⊥平面CDF;
(Ⅱ)分割成两个棱锥,VC-DEF=
S△DEF×CD=
×
×1×
×1=
,VF-ABCD=
SABCD×d=
×2×1×
=
,然后求和.
(Ⅱ)分割成两个棱锥,VC-DEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
解答:
解:(Ⅰ)∵平面ABCD⊥平面ADEF,CD⊥AD,
∴CD⊥平面ADEF,∴CD⊥AF
又AD=2,AF=1,∠DAF=60°,
由余弦定理知DF=
,
∴AF2+DF2=AD2,∴AF⊥DF,
∵DF∩CD=D,
∴AF⊥平面CDF.(6分)
(Ⅱ)在等腰梯形ADEF中,EF=1,两底间的距离d=
,VC-DEF=
S△DEF×CD=
×
×1×
×1=
,
VF-ABCD=
SABCD×d=
×2×1×
=
,
∴VABCDEF=VC-DEF+VF-ABCD=
.(13分) (亦可将几何体补成棱柱求解)
∴CD⊥平面ADEF,∴CD⊥AF
又AD=2,AF=1,∠DAF=60°,
由余弦定理知DF=
| 3 |
∴AF2+DF2=AD2,∴AF⊥DF,

∵DF∩CD=D,
∴AF⊥平面CDF.(6分)
(Ⅱ)在等腰梯形ADEF中,EF=1,两底间的距离d=
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
VF-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴VABCDEF=VC-DEF+VF-ABCD=
5
| ||
| 12 |
点评:本题主要考查了直线与平面垂直的判定,以及着重考查了利棱锥的体积公式求组合几何体的体积问题,考查空间想象能力、运算能力.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.