题目内容
6.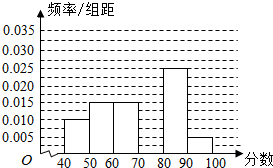 某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)估计本次考试物理成绩的众数与中位数;
(3)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试数学成绩的平均分.
分析 (1)根据频率分布直方图,能求出分数在[70,80)内的频率,并能作出频率分布直方图.
(2)由众数是最高小矩形中点的横坐标,能求出众数,由中位数要平分直方图的面积,能求出中位数.
(3)利用组中值能估算抽样学生的平均分.
解答 解:(1)设分数在[70,80)内的频率为x,
根据频率分布直方图,则有:
(0.01+0.015×2+0.025+0.005)×10+x=1,解得x=0.3,
∴分数在[70,80)内的频率为0.3.
频率分布直方图如图所示.
(2)∵分数在[70,80)内的小矩形最高,众数是最高小矩形中点的横坐标,
∴众数为75.
∵分数在[40,70)内的频率为:(0.01+0.015+0.015)×10=0.4,
∴中位数在(70,80]内,
∵中位数要平分直方图的面积,∴中位数为:70+$\frac{0.5-0.4}{0.03}$=73.3.
(3)利用组中值估算抽样学生的平均分为:
45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
估计这次考试的平均分是71分.
点评 本题考查频率分布直方图的应用及作法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
1.对a,b∈R,记min{a,b}=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,函数f(x)=min{-|x|,-x2+4x+6}的最大值是( )
| A. | 6 | B. | 1 | C. | 0 | D. | $\frac{3-\sqrt{33}}{2}$ |
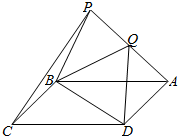 如图所示,点P是平行四边形ABCD所在平面外的一点,点Q是PA的中点,试判断直线PC与平面QBD的位置关系.
如图所示,点P是平行四边形ABCD所在平面外的一点,点Q是PA的中点,试判断直线PC与平面QBD的位置关系.