题目内容
17.将函数y=sin(x+$\frac{π}{6}$)(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的$\frac{1}{2}$,再把图象上各点向左平移$\frac{π}{4}$个单位长度,则所得的图象的解析式为( )| A. | y=sin(2x+$\frac{5}{6}π$) | B. | y=sin($\frac{1}{2}$x+$\frac{1}{6}$π) | C. | y=sin(2x+$\frac{2}{3}$π) | D. | y=sin($\frac{1}{2}$x+$\frac{5}{12}$π) |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数y=sin(x+$\frac{π}{6}$)(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的$\frac{1}{2}$,
可得y=sin(2x+$\frac{π}{6}$)的图象,
再把图象上各点向左平移$\frac{π}{4}$个单位长度,
则所得的图象的解析式为y=sin[2(x+$\frac{π}{4}$)+$\frac{π}{6}$]=sin(2x+$\frac{π}{6}$+$\frac{π}{2}$)=sin(2x+$\frac{2π}{3}$),
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,则BD1与平面ABCD所成的角的大小是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.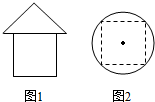 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )| A. | $2\sqrt{2}π+20$ | B. | $\frac{{2\sqrt{2}π}}{3}+8$ | C. | $({2\sqrt{2}+2})π+16$ | D. | $2\sqrt{2}π+16$ |
2.过抛物线x2=4y的焦点任作一直线l交抛物线于M,N两点,O为坐标原点,则△MON的面积的最小值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
9.设集合A={x|x2-3x-4>0},集合B={x|-2<x<5},则A∩B=( )
| A. | {x|-1<x<4} | B. | {x|-2<x<-1或4<x<5} | C. | {x|x<-1或x>4} | D. | {x|-2<x<5} |
6.已知抛物线y2=4x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}=3\overrightarrow{FB}$,O为坐标原点,则△AOB的面积为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |