题目内容
14.已知函数f(x)=|x-2|.(1)解不等式f(x+1)+f(x+2)<4;
(2)若?x∈R使得f(ax)+|a|f(x)≤4成立,求实数a的取值范围.
分析 (1)问题转化为解不等式|x-1|+|x|<4,通过讨论x的范围求出不等式的解集即可;
(2)求出f(ax)+|a|•f(x)的最小值,得到|2a-2|≤4,解出即可.
解答 解:(1)f(x+1)+f(x+2)<4,
即|x-1|+|x|<4,
①x≤0时,不等式为:1-x-x<4,即:x>-$\frac{3}{2}$,
∴-$\frac{3}{2}$<x≤0是不等式的解;
②0<x≤1时,不等式为:1-x+x<4,即1<4化成了,
∴0<x≤1是不等式的解;
③x>1时,不等式为:x-1+x<4,即x<$\frac{5}{2}$,
∴1<x<$\frac{5}{2}$是不等式的解,
综上,不等式的解集是(-$\frac{3}{2}$,$\frac{5}{2}$);
(2)∵f(ax)+|a|•f(x)
=|ax-2|+|a|•|x-2|
=|ax-2|+|2a-ax|≥|ax-2+2a-ax|=|2a-2|,
∴f(ax)+|a|•f(x)的最小值是|2a-2|,
又?x∈R,使得f(ax)+|a|f(x)≤4成立,
∴|2a-2|≤4,
解得:-1≤a≤3.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
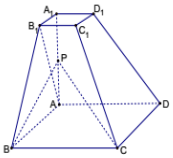 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为AA1的中点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为AA1的中点.