题目内容
4.已知f(x)是R上的奇函数,当x>0时,f(x)=x${\;}^{\frac{1}{2}}$,则f(-9)=-3.分析 先由x>0时,f(x)=x${\;}^{\frac{1}{2}}$,求出f(9),再根据f(x)是R上的奇函数,得到答案.
解答 解:∵当x>0时,f(x)=x${\;}^{\frac{1}{2}}$,
∴f(9)=3,
∵f(x)是R上的奇函数,
∴f(-9)=-f(9)=-3,
故答案为:-3
点评 本题考查的知识点是函数奇偶性的性质,函数求值,难度不大,属于基础题.

练习册系列答案
相关题目
15.若$\frac{cos2α}{sinα-cosα}$=-$\frac{1}{2}$,则sin(α+$\frac{π}{4}$)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{2}}{4}$ |
12.在极坐标系中,点(1,$\frac{π}{4}$)与点(1,$\frac{3π}{4}$)的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
13.执行如图所示的程序框图,输出的S值为( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
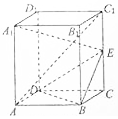 在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证:
在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证: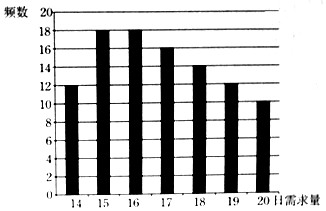 某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.