题目内容
设函数f（x）=
的定义域为A，函数g（x）=
的定义域为B，若A∩B=∅，求实数a的取值范围．
|
| 1 | ||
|
考点：绝对值不等式的解法,其他不等式的解法
专题：不等式的解法及应用
分析：通过分式不等式的解法求出集合A，绝对值不等式的解法求出集合B，利用A∩B=∅，求实数a的取值范围．
解答：
解：函数f（x）=
的定义域为A，
∴
≥0，解得：-4≤x＜2．
∴A={x|-4≤x＜2}．
函数g（x）=
的定义域为B，
∴a-|x-4|＞0，解得-a-4＜x＜a+4，
∴B={x|-a-4＜x＜a+4}．
∵A∩B=∅，
∴a+4＜-4或-a-4≥2，
解得a＜-8或a≤-6，
实数a的取值范围（-∞，-8）．
|
∴
| x+4 |
| 2-x |
∴A={x|-4≤x＜2}．
函数g（x）=
| 1 | ||
|
∴a-|x-4|＞0，解得-a-4＜x＜a+4，
∴B={x|-a-4＜x＜a+4}．
∵A∩B=∅，
∴a+4＜-4或-a-4≥2，
解得a＜-8或a≤-6，
实数a的取值范围（-∞，-8）．
点评：本题考查函数的定义域，分式不等式以及绝对值不等式的解法，集合的交集的应用，考查转化思想以及计算能力．
练习册系列答案
相关题目
设n为正整数，(x-
)2n展开式中存在常数项，则n的一个可能取值为（ ）
| 1 | ||
x
|
| A、16 | B、10 | C、4 | D、2 |
函数f（x）=
的定义域为（ ）
1-
|
| A、{x|0＜x≤1} |
| B、{x|x＜0或x≥1} |
| C、{x|-1＜x＜1} |
| D、∅ |
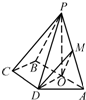如图，已知四棱锥P-ABCD，底面ABCD是等腰梯形，且AB∥CD，O是AB中点，PO⊥平面ABCD，PO=CD=DA=