题目内容
当-1≤x≤1时,函数y=2x2-2ax+1-2a有最小值是-
,则a的值为( )
| 3 |
| 2 |
A、
| ||
| B、1 | ||
| C、3 | ||
| D、1或3 |
考点:二次函数在闭区间上的最值
专题:分类讨论,函数的性质及应用
分析:按照对称轴与区间[-1,1]的位置关系分三种情况进行讨论求得函数的最小值,令其等于-
,解得a值.
| 3 |
| 2 |
解答:
解:函数y=2x2-2ax+1-2a图象的对称轴为x=
,
(1)当
<-1,即a<-2时,ymin=2×(-1)2-2a×(-1)+1-2a=3≠-
,不成立;
(2)当-1≤
≤1,即-2≤a≤2时,ymin=2×(
)2-2a×
+1-2a=-
a2-2a+1=-
,
即
a2+2a-
=0,解得a=1或-5(舍),
(3)当
>1,即a>2时,ymin=2×12-2a×1+1-2a=3-4a=-
,
解得a=
(舍);
综上,a=1,
故选B.
| a |
| 2 |
(1)当
| a |
| 2 |
| 3 |
| 2 |
(2)当-1≤
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即
| 1 |
| 2 |
| 5 |
| 2 |
(3)当
| a |
| 2 |
| 3 |
| 2 |
解得a=
| 9 |
| 8 |
综上,a=1,
故选B.
点评:本题考查二次函数在闭区间上的最值问题,考查分类讨论思想.

练习册系列答案
相关题目
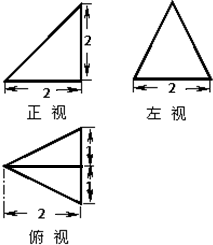 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
设a是函数f(x)=|x2-4|-lnx在定义域内的最小零点,若0<x0<a,则f(x0)的值满足( )
| A、f(x0)>0 |
| B、f(x0)<0 |
| C、f(x0)=0 |
| D、f(x0)的符号不确定 |
 已知函数
已知函数 某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但有一名运动员的身高记录不清楚,其末位数记为x,那么x的值为( )
某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但有一名运动员的身高记录不清楚,其末位数记为x,那么x的值为( )