题目内容
观察下列单项式:x,4x2,9x3,16x4,…,根据你发现的规律,第8个式子是 ,第n个式子是 .
考点:归纳推理
专题:规律型
分析:根据归纳推理的应用,由已知的单项式即可得到规律.
解答:
解:由已知单项式可知x,22x2,32x3,42x4,…,
∴由归纳推理可知第8个式子是82x8=64x8…,
第n个式子是:n2xn.
故答案为:64x8;n2xn.
∴由归纳推理可知第8个式子是82x8=64x8…,
第n个式子是:n2xn.
故答案为:64x8;n2xn.
点评:本题主要考查归纳推理的应用,根据条件观察单项式的规律是解决本题的关键,比较基础.

练习册系列答案
相关题目
下列各数85(9)、1000(4)、111111(2)中最小的数是( )
| A、85(9) |
| B、111111(2) |
| C、1000(4) |
| D、不确定 |
已知cos(
-α)=
,
<a<π,则sin(α+
)=( )
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在直角坐标系中,角α以x轴非负半轴为始边,终边上有一点P(3,4),则cosα=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
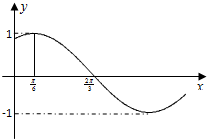 已知函数
已知函数 某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但有一名运动员的身高记录不清楚,其末位数记为x,那么x的值为( )
某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但有一名运动员的身高记录不清楚,其末位数记为x,那么x的值为( )