题目内容
设x=
,y=
,则x3+y3= .
2+
| ||
2-
|
2-
| ||
2+
|
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:直接代入已知条件化简求解即可.
解答:
解:x=
,y=
,
则x3+y3=(
)3+(
)3
=(
+
)[(
+
)2-3×
×
]
=14[142-3]
=14×193
=2702.
故答案为:2702.
2+
| ||
2-
|
2-
| ||
2+
|
则x3+y3=(
2+
| ||
2-
|
2-
| ||
2+
|
=(
2+
| ||
2-
|
2-
| ||
2+
|
2+
| ||
2-
|
2-
| ||
2+
|
2+
| ||
2-
|
2-
| ||
2+
|
=14[142-3]
=14×193
=2702.
故答案为:2702.
点评:本题考查函数值的求法,分解因式的应用,考查计算能力.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
中国古代数学著作《九章算法》中的“更相减损术”可用来求两个正整数的最大公约数.现应用此法求168与93的最大公约数:记(168,93)为初始状态,则第一步可得(75,93),第二步得到(75,18),第三步得到(57,18),第四步将得到( )
| A、(57,18) |
| B、(39,3) |
| C、(39,18) |
| D、(21,18) |
 如图,在△ABC中,BO为边AC上的中线,
如图,在△ABC中,BO为边AC上的中线,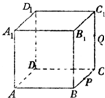 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=