题目内容
若圆M经过点（2，0）、（4，0）、（0，2），求圆M的方程．
考点：圆的一般方程
专题：直线与圆
分析：设出圆的一般式方程，把三个点的坐标代入圆的方程得到方程组，求解D、E、F得答案．
解答：
解：设圆M的方程为x2+y2+Dx+Ey+F=0，
∵圆M经过点（2，0）、（4，0）、（0，2），
∴
，解得：
．
∴圆M的方程为x2+y2-6x+6y+8=0．
∵圆M经过点（2，0）、（4，0）、（0，2），
∴
|
|
∴圆M的方程为x2+y2-6x+6y+8=0．
点评：本题考查了圆的一般式方程，在圆的方程中含有三个待求系数，要求圆的方程，应给出三个独立的条件，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
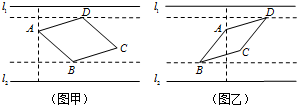如图，某兴趣小组测得菱形养殖区ABCD的固定投食点A到两条平行河岸线l1、l2的距离分别为4米、8米，河岸线l1与该养殖区的最近点D的距离为1米，l2与该养殖区的最近点B的距离为2米．等差数列{an}的前n项和为Sn，若a2+a7+a12=60，则S13的值是（ ）
| A、130 | B、260 |
| C、20 | D、150 |
在平面直角坐标系xOy中设锐角α的始边与x轴的非负半轴重合，终边与单位圆交于点P（x1，y1），将射线OP绕坐标原点O按逆时针方向旋转已知函数y=
的单调增区间是（ ）
| -x2+4x+5 |
| A、（-∞，2] |
| B、[-1，2] |
| C、[2，+∞] |
| D、[2，5] |