题目内容
定义在(-4,4)上的奇函数单调递减,且f(4-2x)+f(x2_4)<f(0),求x的范围.
考点:函数单调性的性质
专题:函数的性质及应用
分析:先用函数的为奇函数,求出f(0)=0,再将不等式移项变形,再利用函数的单调性,得到不等式组,解得即可.
解答:
解:∵函数f(x)在(-4,4)上的奇函数且单调递减,
∴f(0)=0
∵f(4-2x)+f(x2_4)<f(0),得
∴f(x2_4)<-f(4-2x)=f(2x-4),
∴
,
解得2<x<2
故所求范围是:(2,2
)
∴f(0)=0
∵f(4-2x)+f(x2_4)<f(0),得
∴f(x2_4)<-f(4-2x)=f(2x-4),
∴
|
解得2<x<2
| 2 |
故所求范围是:(2,2
| 2 |
点评:本题是对函数单调性和奇偶性的综合考查,只要利用相应性质适当变形即可.

练习册系列答案
相关题目
已知x∈R,则
的最大值是( )
| |12cosx-5sinx+39| |
| 13 |
| A、2 | B、4 | C、13 | D、39 |
 已知集合M={(x,y)|0≤y≤
已知集合M={(x,y)|0≤y≤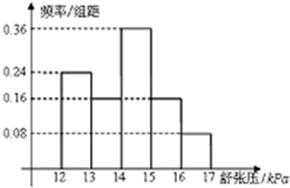 为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为
为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为