题目内容
条件求值:
(1)已知6sin2α+sinαcosα-2cos2α=0,α∈[
,π],求sin(2α+
)的值;
(2)已知tan(
+α)=
(i)求tanα的值
(ii)求
的值.
(1)已知6sin2α+sinαcosα-2cos2α=0,α∈[
| π |
| 2 |
| π |
| 3 |
(2)已知tan(
| π |
| 4 |
| 1 |
| 2 |
(i)求tanα的值
(ii)求
| sin2α-cos2α |
| 1+cos2α |
考点:同角三角函数基本关系的运用,两角和与差的正弦函数,二倍角的正弦
专题:计算题,三角函数的求值
分析:(1)原等式可化简为
sin2α2+2sin2α-12=0,因为2α∈[π,2π]从而可解得sin2α=-
,故cos2α=±
,即可求出sin(2α+
)的值;
(2)(i)由已知可化简得
=
故有tanα=-
.(ii)原式可化简为
=
=
,代入(i)所求即可求值.
| 65 |
| 4 |
| 12 |
| 13 |
| 5 |
| 13 |
| π |
| 3 |
(2)(i)由已知可化简得
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
| 1 |
| 3 |
| sin2α-cos2α |
| 1+cos2α |
| 2sinαcosα-cos2α |
| cos2α |
| 2tanα-1 |
| 2 |
解答:
解:(1)6sin2α+sinαcosα-2cos2α=0
⇒
sin2α-4cos2α+2=0
⇒
sin2α2+2sin2α-12=0
因为α∈[
,π],故2α∈[π,2π]
所以可解得sin2α=-
或者
(舍去)
故cos2α=
=±
所以sin(2α+
)=
sin2α+
cos2α=
或
.
(2)(i)tan(
+α)=
⇒
=
⇒
=
⇒tanα=-
.
(ii)
=
=
=-
.
⇒
| 1 |
| 2 |
⇒
| 65 |
| 4 |
因为α∈[
| π |
| 2 |
所以可解得sin2α=-
| 12 |
| 13 |
| 52 |
| 65 |
故cos2α=
| 1-sin22α |
| 5 |
| 13 |
所以sin(2α+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
5
| ||
| 26 |
-5
| ||
| 26 |
(2)(i)tan(
| π |
| 4 |
| 1 |
| 2 |
tan
| ||
1-tan
|
| 1 |
| 2 |
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
| 1 |
| 3 |
(ii)
| sin2α-cos2α |
| 1+cos2α |
| 2sinαcosα-cos2α |
| cos2α |
| 2tanα-1 |
| 2 |
| 5 |
| 6 |
点评:本题主要考察了同角三角函数基本关系的运用,两角和与差的正弦函数公式,二倍角的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
已知向量
=(2k-3,-6),
=(2,1)且
∥
则实数k=( )
| a |
| c |
| a |
| c |
A、-
| ||
B、
| ||
| C、15 |
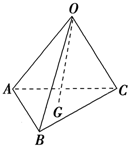 如图,在三棱锥O-ABC中,G是△ABC的重心,若
如图,在三棱锥O-ABC中,G是△ABC的重心,若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
A、
| ||||||
B、
| ||||||
| C、a+b+c | ||||||
| D、3a+3b+3c |
已知函数y=2x,g(x)=f(x-2)-1,若g(a)<1<f(a),则实数a的取值范围为( )
| A、(-∞,0)∪(3,+∞) |
| B、(-∞,0) |
| C、(0,3) |
| D、(0,+∞) |
若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
,则直线l的斜率的取值范围是( )
| 2 |
A、[2-
| ||||||
B、[2-
| ||||||
C、[
| ||||||
| D、[0,+∞) |