题目内容
已知f(x)=x-
,若对于任意的x1,x2∈[2,3],都有|f(x1)-f(x2)|≤a成立,则a的取值范围是 .
| 1 |
| x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:因为|f(x1)-f(x2)|≤a恒成立,所以只需|f(x1)-f(x2)|max≤a即可,因为x1,x2∈[2,3],且是同一个函数,所以只需研究函数f(x)在区间[2,3]上的最值即可.利用单调性容易解决问题.
解答:
解:因为f(x)=x-
,所以f′(x)=1+
>0恒成立,所以函数f(x)在[2,3]上单调递增,
所以f(x)min=f(2)=
,f(x)max=f(3)=
.
因为|f(x1)-f(x2)|≤a恒成立,所以只需|f(x1)-f(x2)|max≤a即可,因为x1,x2∈[2,3],且是同一个函数,
所以只需a≥f(x)max-f(x)min=
-
=
..
即a≥
.
故答案为a≥
..
| 1 |
| x |
| 1 |
| x2 |
所以f(x)min=f(2)=
| 3 |
| 2 |
| 8 |
| 3 |
因为|f(x1)-f(x2)|≤a恒成立,所以只需|f(x1)-f(x2)|max≤a即可,因为x1,x2∈[2,3],且是同一个函数,
所以只需a≥f(x)max-f(x)min=
| 8 |
| 3 |
| 3 |
| 2 |
| 7 |
| 6 |
即a≥
| 7 |
| 6 |
故答案为a≥
| 7 |
| 6 |
点评:本题考查了不等式的恒成立问题,主要是转化为函数的最值问题来解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知复数z满足
(1-i)=2,则z5=( )
. |
| z |
| A、16 | B、-4+4i |
| C、-16 | D、-16i |
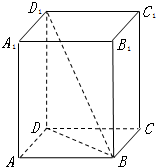 如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B=
如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B=