题目内容
关于x的方程x2-2x+lg（a+1）=0有负实数根，则实数a的取值范围为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：先判断该函数取得实数根的情况，根据韦达定理可以判断出该方程有一正根一负根，所以便得到
，解该不等式组即得实数a的取值范围．
|
解答：
解：根据韦达定理方程x2-2x+lg（a+1）=0的两根之和为2＞0；
∴该方程应有两个实根，一正一负；
∴
，解得-1＜a＜0；
∴实数a的取值范围为：（-1，0）．
故答案为：（-1，0）．
∴该方程应有两个实根，一正一负；
∴
|
∴实数a的取值范围为：（-1，0）．
故答案为：（-1，0）．
点评：考查韦达定理，一元二次方程取得实根的情况和判别式△的关系．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图是一个空间几何体的三视图，则这个几何体的侧面积是（ ）
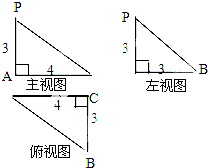
| A、42 | B、21 | C、24 | D、6 |
数列{an}满足an+1-an+an-1=0（n≥2），且a1=1，a2=-1，则a2013的值为（ ）
| A、1 | B、-1 | C、2 | D、-2 |
已知函数f（x）是定义在（0，+∞）上的单调函数，且对任意的正数x，y都有f（x•y）=f（x）+f（y），若数列{an}的前n项和为Sn，且满足f（Sn+2）-f（an）=f（3）（n∈N*），则an为（ ）
| A、2n-1 | ||
| B、n | ||
| C、2n-1 | ||
D、（
|
已知a=log23+log2
， b=
log23， c=log32，则a，b，c大小关系为（ ）
| 3 |
| 1 |
| 2 |
| A、b＜a＜c |
| B、c＜a＜b |
| C、a＜b＜c |
| D、c＜b＜a |