题目内容
7.现有一根n节的竹竿,自上而下每节的长度依次构成等差数列,已知最上面三节的长度之和为36,最下面三节的长度之和为114,整个竹竿的长度为400,则n=16.分析 利用等差数列的性质及其前n项和公式即可得出.
解答 解:由题意可设此数列为{an},其前n项和为Sn.
则a1+a2+a3=36,an-2+an-1+an=114,Sn=400.
∴3(a1+an)=36+114,可得a1+an=50.
∴400=$\frac{n({a}_{1}+{a}_{n})}{2}$=$\frac{50n}{2}$,解得n=16.
故答案为:16.
点评 本题考查了等差数列的性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.设函数f(x)=2sin(ωx-$\frac{π}{3}$),已知f(α)=-2,f(β)=0,且|α-β|的最小值是$\frac{π}{4}$,现将y=f(x)的图象向左平移φ(φ>0)个单位,所得函数图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{5π}{12}$ |
2.设命题p:函数y=-xsinx的图象关于原点对称,
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
12.执行如图的程序框图,如果输入的t∈[-1,π],则输出的S属于( )
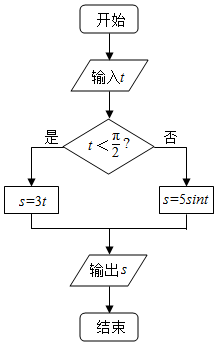

| A. | $[-3,\frac{3π}{2}]$ | B. | $[-5,\frac{3π}{2}]$ | C. | [-5,5] | D. | [-3,5] |
19.在△ABC中,角A、B、C所对的边分别为a、b、c.若c=3,$C=\frac{π}{3}$,且a+b=4,则△ABC的面积为( )
| A. | $\frac{7\sqrt{3}}{12}$ | B. | $\frac{7\sqrt{3}}{4}$ | C. | $\frac{7}{12}$ | D. | $\frac{5\sqrt{3}}{12}$ |