题目内容
17．已知集合A={x|x2-5x-6＜0}，集合B={x|6x2-5x+1≥0}，集合C={x|（x-m）（m+9-x）＞0}（1）求A∩B
（2）若A∪C=C，求实数m的取值范围．
分析 分别解出A，B，C，（1）利用集合运算性质可得A∩B；
（2）由A∪C=C，可得A⊆C．即可得出．
解答 解：由合A={x|x2-5x-6＜0}，集合B={x|6x2-5x+1≥0}，集合C={x|（x-m）（m+9-x）＞0}．
∴A={x|-1＜x＜6}，$B=\left\{{x\left|{x≥\frac{1}{2}或x≤\frac{1}{3}}\right.}\right\}$，C={x|m＜x＜m+9}．
（1）$A∩B=\left\{{x\left|{-1＜x≤\frac{1}{3}或\frac{1}{2}≤x＜6}\right.}\right\}$，
（2）由A∪C=C，可得A⊆C．
即$\left\{{\begin{array}{l}{m+9≥6}\\{m≤-1}\end{array}}\right.$，解得-3≤m≤-1．
点评 本题考查了不等式的解法、集合运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
5．已知球O的一个内接三棱锥P-ABC，其中△ABC是边长为2的正三角形，PC为球O的直径，且PC=4，则此三棱锥的体积为（ ）
| A． | $\frac{2}{3}\sqrt{3}$ | B． | $\frac{4}{3}\sqrt{2}$ | C． | $\frac{4}{3}\sqrt{6}$ | D． | $\frac{2}{3}\sqrt{6}$ |
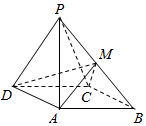如图，四棱锥P-ABCD中，侧面PDC是正三角形，底面ABCD是边长为$2\sqrt{3}$的菱形，∠DAB=120°，且侧面PDC与底面垂直，M为PB的中点．
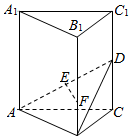在正三棱柱ABC-A1B1C1中，AB=AA1=1，DC=DC1，AE=ED，F为BB1上任意一点，且FB1=3BF．
9．已知点A是抛物线C：x2=2py（p＞0）上一点，O为坐标原点，若以点M（0，8）为圆心，|OA|的长为半径的圆交抛物线C于A，B两点，且△ABO为等边三角形，则p的值是（ ）
| A． | $\frac{3}{8}$ | B． | 2 | C． | 6 | D． | $\frac{2}{3}$ |