题目内容
15.设函数f(x)=2sin(ωx-$\frac{π}{3}$),已知f(α)=-2,f(β)=0,且|α-β|的最小值是$\frac{π}{4}$,现将y=f(x)的图象向左平移φ(φ>0)个单位,所得函数图象关于y轴对称,则φ的最小值是( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{5π}{12}$ |
分析 由条件利用正弦函数的图象和性质求得函数的解析式,再根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性求得φ的最小值.
解答 解:设函数f(x)=2sin(ωx-$\frac{π}{3}$),已知f(α)=-2,f(β)=0,且|α-β|的最小值是$\frac{π}{4}$,
∴$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{π}{4}$,∴ω=2,f(x)=2sin(2x-$\frac{π}{3}$).
且2α-$\frac{π}{3}$=2kπ-$\frac{π}{2}$,2β-$\frac{π}{3}$=2kπ+0,k∈Z.
现将y=f(x)的图象向左平移φ(φ>0)个单位,
所得函数y=2sin[2(x+φ)-$\frac{π}{3}$]=2sin(2x+2φ-$\frac{π}{3}$)的图象.
根据所得关于y轴对称,可得2φ-$\frac{π}{3}$=nπ+$\frac{π}{2}$,即φ=$\frac{nπ}{2}$+$\frac{5π}{12}$,n∈Z,则φ的最小值是$\frac{5π}{12}$,
故选:D.
点评 本题主要考查正弦函数的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
5.已知球O的一个内接三棱锥P-ABC,其中△ABC是边长为2的正三角形,PC为球O的直径,且PC=4,则此三棱锥的体积为( )
| A. | $\frac{2}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{2}$ | C. | $\frac{4}{3}\sqrt{6}$ | D. | $\frac{2}{3}\sqrt{6}$ |
10.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(2,m),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
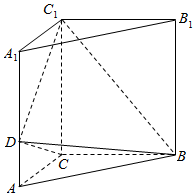 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{2}{5}$AA1,D是棱AA1上的点,且AD=$\frac{1}{4}$DA1.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{2}{5}$AA1,D是棱AA1上的点,且AD=$\frac{1}{4}$DA1.


