题目内容
13. 如图,正三棱柱ABC-A1B1C1所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H.
如图,正三棱柱ABC-A1B1C1所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H.(Ⅰ)求证:AE⊥平面A1BD;
(Ⅱ)求二面角D-BA1-A的余弦值;
(Ⅲ)求A1B1与平面A1BD所成的角的正弦值.
分析 以D为原点,DA为x轴正半轴,DB为z轴正半轴建立如图所示空间直角坐标系,利用向量法求解.
解答 解:(Ⅰ)以D为原点,DA为x轴正半轴,DB为z轴正半轴建立如图所示空间直角坐标系,
则$\overrightarrow{AE}$=(-2,-1,0),$\overrightarrow{{A}_{1}D}$=(-1,2,0),$\overrightarrow{BD}=(0,0,-\sqrt{3})$,
∵$\overrightarrow{AE}$•$\overrightarrow{{A}_{1}D}$=2-2=0,$\overrightarrow{AE}•\overrightarrow{BD}$=$0+0+0({-\sqrt{3}})=0$,∴$\overrightarrow{AE}⊥\overrightarrow{{A_1}D}$,$\overrightarrow{AE}⊥\overrightarrow{BD}$,
即AE⊥A1D,AE⊥BD,∴AE⊥面A1BD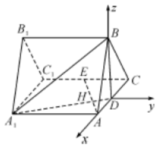
(Ⅱ)由(Ⅰ)可知$\overrightarrow{n_1}=\overrightarrow{AE}$=(-2,-1,0)即为面A1BD的一个法向量.
设面AA1B的法向量为$\overrightarrow{n_2}=({{x_2},{y_2},{z_2}})$则有$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{{A_1}B}=0\\ \overrightarrow{n_2}•\overrightarrow{{A_1}A}=0\end{array}\right.$得$\left\{\begin{array}{l}-{x_2}+2{y_2}+\sqrt{3}{z_2}=0\\ 2{y_2}=0\end{array}\right.$
取$\overrightarrow{n_2}=({3,0,\sqrt{3}})$,$cos\left?{\overrightarrow{n_1},\overrightarrow{n_2}}\right>=\frac{6}{{\sqrt{5}•\sqrt{12}}}$=$\frac{{\sqrt{15}}}{5}$
由图可知二面角D-BA1-A为锐二面角,∴它的余弦值为$\frac{{\sqrt{15}}}{5}$
(Ⅲ)B1B=(0,2,0),平面A1BD的法向量取$\overrightarrow{n_1}=\overrightarrow{AE}$=(-2,-1,0)
则B1到平面A1BD的距离$d=\frac{{|{\overrightarrow{{B_1}B}•\overrightarrow{n_1}}|}}{{|{\overrightarrow{n_1}}|}}$=$\frac{{2\sqrt{5}}}{5}$
设A1B1与平面A1BD所成的角为θ,则$sinθ=\frac{d}{{{A_1}{B_1}}}$=$\frac{{\frac{{2\sqrt{5}}}{5}}}{2}=\frac{{\sqrt{5}}}{5}$
点评 本题考查了空间向量的应用,考查了计算能力、转化思想,属于中档题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案| A. | (-0.025,0.025) | B. | (0,0.025) | C. | (0.025,1) | D. | (-0.025,0) |
| A. | (0,π) | B. | $({0,\frac{π}{4}})$ | C. | $[{0,\frac{π}{4}})∪({\frac{3}{4}π,π})$ | D. | $[{0,\frac{π}{4}})∪({\frac{π}{2},π})$ |