题目内容
椭圆C1以双曲线C2:
-
=1的实轴为短轴、虚轴为长轴,且与抛物线C3:y2=12x交于A,B两点.
(Ⅰ)求椭圆C1的方程及线段AB的长;
(Ⅱ)在C1与C3图象的公共区域内,是否存在一点P(x0,y0),使得C1的弦EF与C3的弦MN相互垂直平分于点P?若存在,求点P坐标,若不存在,说明理由.
| x2 |
| 4 |
| y2 |
| 16 |
(Ⅰ)求椭圆C1的方程及线段AB的长;
(Ⅱ)在C1与C3图象的公共区域内,是否存在一点P(x0,y0),使得C1的弦EF与C3的弦MN相互垂直平分于点P?若存在,求点P坐标,若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:计算题,转化思想,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用双曲线与椭圆的关系,直接求椭圆C1的方程,联立椭圆与抛物线方程求出交点坐标,即可求出线段AB的长;
(Ⅱ)设出弦EF端点的坐标代入椭圆方程,利用平方差法求出EF的斜率,讨论求出弦MN的斜率,利用相互垂直,推出关系式,说明点P不在区域内即可.
(Ⅱ)设出弦EF端点的坐标代入椭圆方程,利用平方差法求出EF的斜率,讨论求出弦MN的斜率,利用相互垂直,推出关系式,说明点P不在区域内即可.
解答:
解:(Ⅰ)∵椭圆C1以双曲线C2:
-
=1的实轴为短轴、虚轴为长轴,
∴椭圆C1:
+
=1;
联立方程组
解得:
,
∴A(1,2
),B(1,-2
),
∴|AB|=4
.
(Ⅱ)假设存在,设E(x1,y1),F(x2,y2),
由题意将E,F坐标带入C1,
+
=1,
+
=1
作差得:
=
(
-
),
kEF=
,
∵x1+x2=2x0,y1+y2)=2y0,
∴kEF=-
=-4
,
同理将M,N坐标带入C3得kMN=
,
∵kEF•kMN=-1,∴
=24x0>12x0,
故满足条件的P点在抛物线C3外,
∴不存在这样的点P.
| x2 |
| 4 |
| y2 |
| 16 |
∴椭圆C1:
| x2 |
| 4 |
| y2 |
| 16 |
联立方程组
|
|
∴A(1,2
| 3 |
| 3 |
∴|AB|=4
| 3 |
(Ⅱ)假设存在,设E(x1,y1),F(x2,y2),
由题意将E,F坐标带入C1,
| x12 |
| 4 |
| y12 |
| 16 |
| x22 |
| 4 |
| y22 |
| 16 |
作差得:
| x | 2 1 |
| -x | 2 2 |
| 1 |
| 4 |
| y | 2 1 |
| y | 2 2 |
kEF=
| y1-y2 |
| x1-x2 |
∵x1+x2=2x0,y1+y2)=2y0,
∴kEF=-
| 16 |
| 4 |
| x0 |
| y0 |
| x0 |
| y0 |
同理将M,N坐标带入C3得kMN=
| 6 |
| y0 |
∵kEF•kMN=-1,∴
| y | 2 0 |
故满足条件的P点在抛物线C3外,
∴不存在这样的点P.
点评:本题考查椭圆方程的求法,直线与椭圆双曲线以及抛物线的位置关系,直线的垂直体积的应用,考查分析问题解决问题的能力;考查设而不求平方差法以及转化思想的应用.

练习册系列答案
相关题目
执行如图所示的程序框图,输入的N=2014,则输出的S=( )


| A、2011 | B、2012 |
| C、2013 | D、2014 |
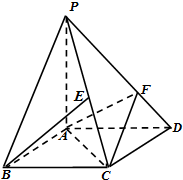 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD. 某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有
某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).