题目内容
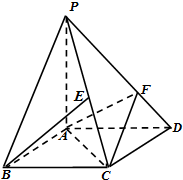 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD.(Ⅰ)求证:BE∥平面ACF;
(Ⅱ)设二面角A-CF-D的大小为θ,若|cosθ|=
| ||
| 14 |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间向量及应用
分析:(Ⅰ)由已知条件用余弦定理和勾股定理推导出AB⊥AC.又PA⊥面ABCD,以AB,AC,AP分别为x,y,z轴建立坐标系.利用向量法能求出BE∥平面ACF.
(Ⅱ)分别求出面PCD法向量和面ACF的法向量,由|cosθ|=
,利用向量法能求出PA的长.
(Ⅱ)分别求出面PCD法向量和面ACF的法向量,由|cosθ|=
| ||
| 14 |
解答:
 (Ⅰ)证明:∵由AD=2,AB=1,ABCD是平行四边形,∠ABC=60°,
(Ⅰ)证明:∵由AD=2,AB=1,ABCD是平行四边形,∠ABC=60°,
∴AC=
=
,
∴AB⊥AC.
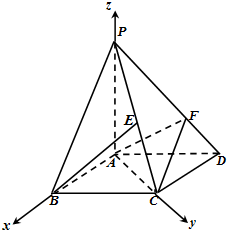
又∵PA⊥面ABCD,∴以AB,AC,AP分别为x,y,z轴建立坐标系.
则A(0,0,0),B(1,0,0),C(0,
,0),D(-1,
,0),
设P(0,0,c),则E(0,
,
).
设F(x,y,z),∵PF=2FD,
∴
=2
,即:(x,y,z-c)=2(-1-x,
-y,-z).
解得:x=-
,y=
,z=
,
∴F(-
,
,
).…..(5分)
∴
=(-
,
,
),
=(0,
,0),
=(-1,
,
).
设面ACF的法向量为
=(x,y,z),
则
,取
=(c, 0, 2).
因为
•
=-c+c=0,且BE?面ACF,
∴BE∥平面ACF. …..(9分)
(Ⅱ)设面PCD法向量为
=(x,y,z),
∵
=(0,
, -c),
=(-1,
, -c),
∴
,取
=(0, c,
). …..(11分)
由|cosθ|=|
|=
,得
=
.
整理,得c4+7c2-44=0,解得c=2,
∴PA=2. …..(15分)
 (Ⅰ)证明:∵由AD=2,AB=1,ABCD是平行四边形,∠ABC=60°,
(Ⅰ)证明:∵由AD=2,AB=1,ABCD是平行四边形,∠ABC=60°,∴AC=
| 4+1-2×2×1×cos60° |
| 3 |
∴AB⊥AC.
又∵PA⊥面ABCD,∴以AB,AC,AP分别为x,y,z轴建立坐标系.
则A(0,0,0),B(1,0,0),C(0,
| 3 |
| 3 |
设P(0,0,c),则E(0,
| ||
| 2 |
| c |
| 2 |
设F(x,y,z),∵PF=2FD,
∴
| PF |
| FD |
| 3 |
解得:x=-
| 2 |
| 3 |
2
| ||
| 3 |
| c |
| 3 |
∴F(-
| 2 |
| 3 |
2
| ||
| 3 |
| c |
| 3 |
∴
| AF |
| 2 |
| 3 |
2
| ||
| 3 |
| c |
| 3 |
| AC |
| 3 |
| BE |
| ||
| 2 |
| c |
| 2 |
设面ACF的法向量为
| n |
则
|
| n |
因为
| n |
| BE |
∴BE∥平面ACF. …..(9分)
(Ⅱ)设面PCD法向量为
| m |
∵
| PC |
| 3 |
| PD |
| 3 |
∴
|
| m |
| 3 |
由|cosθ|=|
| ||||
|
|
| ||
| 14 |
2
| ||||
|
| ||
| 14 |
整理,得c4+7c2-44=0,解得c=2,
∴PA=2. …..(15分)
点评:本题考查直线与平面平行的证明,考查线段长的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题中,真命题是( )
| A、命题“若p,则q”的否命题是“若p,则¬q” | ||
B、a+b=0的充要条件是
| ||
| C、已知命题p、q,若“p∨q”为假命题,则命题p与q一真一假 | ||
| D、命题p:?x∈R,使得x2+1<0,则¬p:?x∈R,使得x2+1≥0 |
若复数m(m-1)+(m2-3m+2)i是纯虚数(其中i为虚数单位),则m=( )
| A、0或1 | B、1 | C、0 | D、1或2 |
