题目内容
P是棱长为1的正四面体内任一点,则P点到四个面的距离之和为 .
考点:棱锥的结构特征
专题:计算题,空间位置关系与距离
分析:用特例法解选择题,设P为正四面体的中心,求出由棱长为1时P点到四个面的距离之和,这样可得选择题的答案.
解答:
 解:设P为正四面体的中心,如图F为CD的中点,AE⊥平面BCD,
解:设P为正四面体的中心,如图F为CD的中点,AE⊥平面BCD,
∴E为△BCD的中心,由棱长为1可以得到BF=
,BE=
×
=
,
AE=
=
,
BP=AP=
-PE,
在直角三角形中,根据勾股定理可以得到BP2=BE2+PE2,
把数据代入得到PE=
,
根据正四面体的中心到各面的距离相等,
∴P点到四个面的距离之和为4×
=
.
当P为正四面体内任一点,P点到四个面的距离之和均为
故答案为:
.
 解:设P为正四面体的中心,如图F为CD的中点,AE⊥平面BCD,
解:设P为正四面体的中心,如图F为CD的中点,AE⊥平面BCD,∴E为△BCD的中心,由棱长为1可以得到BF=
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
AE=
12-(
|
| ||
| 3 |
BP=AP=
| ||
| 3 |
在直角三角形中,根据勾股定理可以得到BP2=BE2+PE2,
把数据代入得到PE=
| ||
| 12 |
根据正四面体的中心到各面的距离相等,
∴P点到四个面的距离之和为4×
| ||
| 12 |
| ||
| 3 |
当P为正四面体内任一点,P点到四个面的距离之和均为
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查了棱锥的结构特征,利用特除情况求解P点到四个面的距离之和是一种常用的解选择题的方法.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
若复数m(m-1)+(m2-3m+2)i是纯虚数(其中i为虚数单位),则m=( )
| A、0或1 | B、1 | C、0 | D、1或2 |
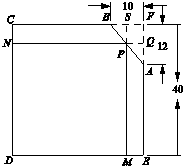 有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)
有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)