题目内容
8.已知F1,F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,Q为椭圆C上的一点,且△QF1O(O为坐标原点)为正三角形,若射线QF1与椭圆交于点P,则△QF1F2与△PF1F2的面积的比值是$\frac{3+2\sqrt{3}}{3}$.分析 作图,结合图象可得c+$\sqrt{3}c$=2a,从而可得椭圆C的方程为$\frac{{x}^{2}}{\frac{2+\sqrt{3}}{2}{c}^{2}}$+$\frac{{y}^{2}}{\frac{\sqrt{3}}{2}{c}^{2}}$=1,再直线方程联立消元可得$\frac{6+4\sqrt{3}}{3}$y2-2cy-$\frac{3}{2}$c2=0,从而可得点Q的纵坐标为$\frac{\sqrt{3}}{2}$c,点P的纵坐标为-$\frac{3\sqrt{3}c}{6+4\sqrt{3}}$,从而解得.
解答 解:由题意作图如右图,
∵△QF1O(O为坐标原点)为正三角形,
∴△QF1F2是直角三角形,
∴c+$\sqrt{3}c$=2a,
∴a=$\frac{\sqrt{3}+1}{2}$c,b2=a2-c2=$\frac{\sqrt{3}}{2}$c2,
∴椭圆C的方程为$\frac{{x}^{2}}{\frac{2+\sqrt{3}}{2}{c}^{2}}$+$\frac{{y}^{2}}{\frac{\sqrt{3}}{2}{c}^{2}}$=1,
设直线PQ的方程为y=$\sqrt{3}$(x+c),
故x=$\frac{\sqrt{3}}{3}$y-c,
代入消x化简可得,
$\frac{6+4\sqrt{3}}{3}$y2-2cy-$\frac{3}{2}$c2=0,
即(y-$\frac{\sqrt{3}}{2}$c)($\frac{6+4\sqrt{3}}{3}$y+$\sqrt{3}c$)=0,
故点Q的纵坐标为$\frac{\sqrt{3}}{2}$c,点P的纵坐标为-$\frac{3\sqrt{3}c}{6+4\sqrt{3}}$,
故△QF1F2与△PF1F2的面积的比值为$\frac{\frac{\sqrt{3}}{2}c}{\frac{3\sqrt{3}c}{6+4\sqrt{3}}}$=$\frac{3+2\sqrt{3}}{3}$,
故答案为:$\frac{3+2\sqrt{3}}{3}$.
点评 本题考查了圆锥曲线与直线的位置关系的应用及数形结合的思想方法应用,属于中档题.

| A. | 4 cm | B. | 5cm | C. | 6cm | D. | 7cm |
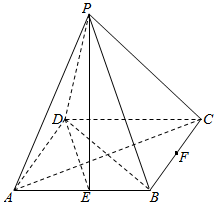 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.