题目内容
3.直线y=2x与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1交于点M(x1,y1),N(x2,y2),则x1x2+y1y2=-$\frac{36}{5}$.分析 由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}=1}\\{y=2x}\end{array}\right.$可得25x2-36=0,从而可得x1x2=-$\frac{36}{25}$,y1y2=4x1x2=-$\frac{36}{25}$×4,从而解得.
解答 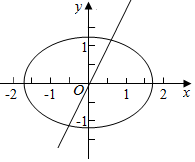 解:由题意得,
解:由题意得,
$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}=1}\\{y=2x}\end{array}\right.$,
化简可得,
25x2-36=0,
由韦达定理可得,
x1x2=-$\frac{36}{25}$,
y1y2=4x1x2=-$\frac{36}{25}$×4,
故x1x2+y1y2=-$\frac{36}{25}$×5=-$\frac{36}{5}$,
故答案为:-$\frac{36}{5}$.
点评 本题考查了圆锥曲线与直线的位置关系的应用及数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
13.向量$\overrightarrow{O{Z_1}}$对应的复数是5-4i,向量$\overrightarrow{O{Z_2}}$对应的复数是-5+4i,则向量$\overrightarrow{{Z_1}{Z_2}}$对应的复数是( )
| A. | -10+8i | B. | 10-8i | C. | -8+10i | D. | 8+-10i |
12.数列a1,a2,…,a7,其中恰好有5个2和2个4,调换a1至a7各数的位置,一共可以组成不同的数列(含原数列( )
| A. | 21个 | B. | 25个 | C. | 32个 | D. | 42个 |
13.已知a>0,b>0,则$\frac{a+b}{2}$,$\sqrt{ab}$,$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$,$\frac{2ab}{a+b}$中最小的是( )
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{ab}$ | C. | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ | D. | $\frac{2ab}{a+b}$ |
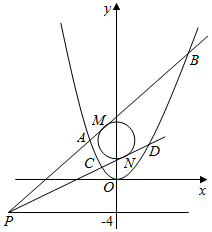 在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.
在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.