题目内容
为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下资料:
(Ⅰ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出y关于x的线性回归方程
=bx+a;
(Ⅱ)若由线性回归方程得到的估计数据与所选出的两组检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(I)中所得的线性回归方程是否可靠?
(参考公式:b=
,a=
-b
)(参考数据:
xiyi=977,
=43.4)
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
| ? |
| y |
(Ⅱ)若由线性回归方程得到的估计数据与所选出的两组检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(I)中所得的线性回归方程是否可靠?
(参考公式:b=
| |||||||
|
. |
| y |
. |
| x |
| 3 |
 |
| i-1 |
| 3 |
 |
| i-1 |
| x | 2 i |
考点:线性回归方程
专题:计算题,概率与统计
分析:(Ⅰ)根据所给的数据,先做出x,y的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程.
(Ⅱ)根据估计数据与所选出的检验数据的误差均不超过2颗,就认为得到的线性回归方程是可靠的,根据求得的结果和所给的数据进行比较,得到所求的方程是可靠的.
(Ⅱ)根据估计数据与所选出的检验数据的误差均不超过2颗,就认为得到的线性回归方程是可靠的,根据求得的结果和所给的数据进行比较,得到所求的方程是可靠的.
解答:
解:(I)由数据得
=12,
=27,3
=972,3
2=432
又
xiyi=977,
═434,∴b=
=
,a=27-
×12=-3
所以y关于x的线性回归方程为
=
x-3…(6分)
(II)当x=10时,
=22,|22-23|<2,当x=8时,
=17,|17-16|<2
所以得到的线性回归方程是可靠的…(12分)
. |
| x |
. |
| y |
. |
| x |
. |
| y |
. |
| x |
又
| 3 |
 |
| i=1 |
| 3 |
 |
| i=1 |
| x | 2 i |
| 977-972 |
| 434-432 |
| 5 |
| 2 |
| 5 |
| 2 |
所以y关于x的线性回归方程为
| ∧ |
| y |
| 5 |
| 2 |
(II)当x=10时,
| ∧ |
| y |
| ∧ |
| y |
所以得到的线性回归方程是可靠的…(12分)
点评:本题考查回归直线方程的计算与应用,在计算线性回归方程时计算量较大,注意正确计算.

练习册系列答案
相关题目
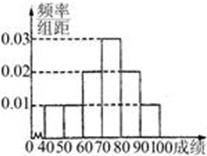 我校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).
我校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).