题目内容
对于有线性相关关系的变量x，y，测得一组数据如表：
根据表，利用最小二乘法得它们的回归直线方程为
=8.5x+
，据此模型来预测x=20时，y的估计值是（ ）
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 60 | 70 |
 |
| y |
|
| a |
| A、170 | B、175.5 |
| C、177.5 | D、212.5 |
考点：线性回归方程
专题：概率与统计
分析：求出横标和纵标的平均数，写出样本中心点，把样本中心点代入线性回归方程，得到关于a的方程，解方程即可．
解答：
解：∵
=
=5，
=
=50
∴这组数据的样本中心点是（5，50）
把样本中心点代入回归直线方程
=8.5x+
，
∴50=8.5×5+a，
∴a=7.5．
=8.5x+7.5，
预测x=20时，y的估计值：
=8.5×20+7.5=177.5．
故选：C．
. |
| x |
| 2+4+5+6+8 |
| 5 |
. |
| y |
| 20+40+60+60+70 |
| 5 |
∴这组数据的样本中心点是（5，50）
把样本中心点代入回归直线方程
|
| y |
|
| a |
∴50=8.5×5+a，
∴a=7.5．
|
| y |
预测x=20时，y的估计值：
|
| y |
故选：C．
点评：本题考查线性回归方程，解题的关键是线性回归直线一定过样本中心点，这是求解线性回归方程的步骤之一．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的离心率为2．F1、F2分别是它的左、右焦点，点A是它的右顶点．过F1作一条斜率为k（k≠0）的直线与双曲线交于两个点M、N．则∠MAN=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、30° | B、45° |
| C、60° | D、90° |
已知M（x，y）落在双曲线
-
=1的两条渐近线与抛物线y2=-2px（p＞0）的准线所围成的封闭区域（包括边界）内，且点M的坐标（x，y）满足x+2y+a=0．若a的最大值为2
-2，则p为（ ）
| y2 |
| 3 |
| x2 |
| 2 |
| 6 |
| A、2 | B、4 | C、8 | D、16 |
若称集合A旳非空真子集的真子集为集合A的“孙子集”，则集合A{A，B，C，D}的“孙子集”有（ ）
| A、16个 | B、15个 |
| C、11个 | D、10个 |
正三角形ABC的边长为2，将它沿高AD翻折，使点B与点C间的距离为
，此时四面体ABCD的外接球的表面积为（ ）
| 2 |
| A、6π | ||
B、
| ||
| C、5π | ||
D、
|
下列命题：
①直线l与平面α无数条直线平行，则l∥α；
②若直线m在平面α外，则m∥α；
③若直线m⊥n，直线n?α内，则m⊥α；
④若直线m∥n，m?α，直线n?β内，那么平面α∥平面β；
其中真命题的个数是为（ ）
①直线l与平面α无数条直线平行，则l∥α；
②若直线m在平面α外，则m∥α；
③若直线m⊥n，直线n?α内，则m⊥α；
④若直线m∥n，m?α，直线n?β内，那么平面α∥平面β；
其中真命题的个数是为（ ）
| A、0 | B、2 | C、3 | D、4 |
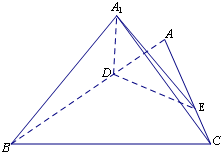已知△ABC是边长为3的等边三角形，点D、E分别是边AB、AC上的点，且满足