题目内容
18.已知△ABC的三个顶点是A(1,1),B(-1,3),C(3,4).(1)求BC边的高所在直线l1的方程;
(2)若直线l2过C点,且A、B到直线l2的距离相等,求直线l2的方程.
分析 (1)利用斜率计算公式、相互垂直的直线斜率之间的关系、点斜式即可得出.
(2)利用斜率计算公式、中点坐标公式、点斜式即可得出.
解答 解:(1)∵${k_{BC}}=\frac{4-3}{3+1}=\frac{1}{4}$,${k}_{{l}_{1}}$=$-\frac{1}{{k}_{BC}}$=-4,…(4分)
∴直线l1的方程是y=-4(x-1)+1,即4x+y-5=0. …(6分)
(2)∵直线l2过C点且A、B到直线l2的距离相等,
∴直线l2与AB平行或过AB的中点M,
∵${k_{AB}}=\frac{3-1}{-1-1}=-1$,∴直线l2的方程是y=-(x-3)+4,即x+y-7=0,…(9分)
∵AB的中点M的坐标为(0,2),
∴${k_{CM}}=\frac{4-2}{3-0}=\frac{2}{3}$,∴直线l2的方程是$y=\frac{2}{3}(x-3)+4$,即2x-3y+6=0,
综上,直线l2的方程是x+y-7=0或2x-3y+6=0. …(12分)
点评 本题考查了斜率计算公式、相互垂直的直线斜率之间的关系、点斜式、中点坐标公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
6.已知集合M={x|x>2},$a=\sqrt{5}$,则下列关系式正确的是( )
| A. | a⊆M | B. | a∉M | C. | {a}∉M | D. | {a}⊆M |
3.空间直角坐标系Oxyz中的点P(1,2,3)在xOy平面内射影是Q,则点Q的坐标为( )
| A. | (1,2,0) | B. | (0,0,3) | C. | (1,0,3) | D. | (0,2,3) |
10.已知直线m,n是平面α,β外的两条直线,且m∥α,n⊥β,α⊥β,则( )
| A. | m∥n | B. | m⊥n | C. | n∥α | D. | n⊥α |
8.已知在等比数列{an}中,a4,a8是方程x2-8x+9=0的两根,则a6为( )
| A. | -3 | B. | ±3 | C. | 3 | D. | 2 |

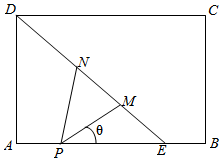 如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN=$\frac{π}{4}$,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN=$\frac{π}{4}$,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.