题目内容
18.已知△ABC的内角A,B,C的对边分别为a,b,c,若a=1,2cosC+c=2b.(Ⅰ)求A;
(Ⅱ)若b=$\frac{1}{2}$,求sinC.
分析 (I)利用余弦定理即可得出.
(II)由b=$\frac{1}{2}$,及b2+c2-1=bc,解得c,再利用正弦定理即可得出.
解答 解:(Ⅰ)∵a=1,2cosC+c=2b.,
由余弦定理得$2×\frac{{1}^{2}+{b}^{2}-{c}^{2}}{2b}$+c=2b,即b2+c2-1=bc.…(2分)
∴cosA=$\frac{{b}^{2}+{c}^{2}-1}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$…(4分)
由于0<A<π,∴A=$\frac{π}{3}$.…(6分)
(Ⅱ)由b=$\frac{1}{2}$,及b2+c2-1=bc,得$\frac{1}{4}+{c}^{2}$-1=$\frac{1}{2}$c,…(7分)
即4c2-2c-3=0,c>0.…(8分)
解得c=$\frac{1+\sqrt{13}}{4}$.…(9分)
由正弦定理得$\frac{c}{sinC}$=$\frac{a}{sinA}$,…(10分)
得sinC=$\frac{1+\sqrt{13}}{4}×sin6{0}^{°}$=$\frac{\sqrt{3}+\sqrt{39}}{8}$.
点评 本题考查了正弦定理余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知集合A,B,C满足A∪B={a,b,c},则满足条件的组合(A,B)共有( )组.
| A. | 4 | B. | 8 | C. | 9 | D. | 27 |
13.若a>0,b>0,且函数f(x)=6x3-ax2-2bx+2在x=1处有极值,若t=ab,则t的最大值为( )
| A. | $\frac{81}{4}$ | B. | 6 | C. | $\frac{81}{2}$ | D. | 9 |
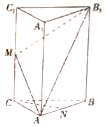 如图,在正三棱柱ABC-A1B1C1中,AB=2,M,N分别是CC1,AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,M,N分别是CC1,AB的中点.