题目内容
10.已知等差数列{an}的前n项和为Sn,并且a2=2,S5=15,数列{bn}满足${b_n}=2-\frac{n+2}{2^n}({n∈{N^+}})$,记集合$M=\left\{{n|\frac{{2{S_n}({2-{b_n}})}}{n+2}≥λ,n∈{N^*}}\right\}$,若M的子集个数为16,则实数λ的取值范围为$\frac{15}{16}$<λ≤1.分析 根据等差数列的通项公式与前n项和求出Sn,化简集合M,构造函数f(n)=$\frac{{n}^{2}+n}{{2}^{n}}$,n∈N*,
研究函数f(n)=$\frac{{n}^{2}+n}{{2}^{n}}$的单调性,求出不等式$\frac{{n}^{2}+n}{{2}^{n}}$≥λ,n∈N+解的个数,
从而得出λ的取值范围.
解答 解:设数列{an}的公差为d,
∵等差数列{an|的前n项和为Sn,并且a2=2,S5=15,
由题意得$\left\{\begin{array}{l}{{a}_{1}+d=2}\\{{5a}_{1}+10d=15}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=1}\end{array}\right.$,
∴an=n,
∴Sn=n+$\frac{n(n-1)}{2}$=$\frac{{n}^{2}+n}{2}$.
∵数列{bn}满足${b_n}=2-\frac{n+2}{2^n}({n∈{N^+}})$,
集合$M=\left\{{n|\frac{{2{S_n}({2-{b_n}})}}{n+2}≥λ,n∈{N^*}}\right\}$,
得$\frac{{(n}^{2}+n)•\frac{n+2}{{2}^{n}}}{n+2}$=$\frac{{n}^{2}+n}{{2}^{n}}$≥λ,n∈N*;
令f(n)=$\frac{{n}^{2}+n}{{2}^{n}}$,n∈N*,
则f(1)=1,f(2)=$\frac{3}{2}$,f(3)=$\frac{3}{2}$,f(4)=$\frac{5}{4}$,f(5)=$\frac{15}{16}$.
下面研究数列f(n)=$\frac{{n}^{2}+n}{{2}^{n}}$的单调性,
∵f(n+1)-f(n)=$\frac{{(n+1)}^{2}+(n+1)}{{2}^{n+1}}$-$\frac{{n}^{2}+n}{{2}^{n}}$=$\frac{(n+1)(2-n)}{{2}^{n+1}}$,
∴n≥3时,f(n+1)-f(n)<0,f(n+1)<f(n),即f(n)单调递减.
∵M的子集个数为16,∴2n=16,解得n=4,
∴集合M的元素个数为4;
∴不等式$\frac{{n}^{2}+n}{{2}^{n}}$≥λ,n∈N+解的个数为4,
∴λ的取值范围是$\frac{15}{16}<λ≤1$.
故答案为:$\frac{15}{16}$<λ≤1.
点评 本题考查了等差数列的通项公式与前n项和公式,数列的单调性与集合的性质,是综合题.

| A. | [$\frac{19π}{4}$,$\frac{27π}{4}$) | B. | [$\frac{9π}{2}$,$\frac{13π}{2}$) | C. | [$\frac{17π}{4}$,$\frac{25π}{4}$) | D. | [4π,6π) |
| A. | (1,2) | B. | [$\frac{1}{2},1$] | C. | ($\frac{1}{2},1$) | D. | (2,3) |
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
| A. | ∅ | B. | {0} | C. | {-1,1} | D. | {-1,0,1} |
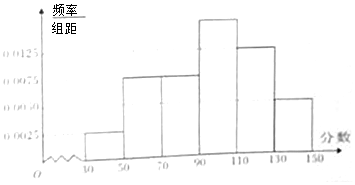 某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图: