题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{-lo{g}_{2}(3-x),x<2}\\{{2}^{x-2}-1,x≥2}\end{array}\right.$,若f(2-a)=1,则f(a)=( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 当2-a≥2,即a≤0时,22-a-2-1=1,从而f(a)=f(-1)=-2;当2-a<2时,得a=-$\frac{1}{2}$,不成立,由此能求出结果.
解答 解:当2-a≥2,即a≤0时,22-a-2-1=1,
解得a=-1,
则f(a)=f(-1)=-log2[3-(-1)]=-2,
当2-a<2,即a>0时,-log2[3-(2-a)]=1,
解得a=-$\frac{1}{2}$,舍去.∴f(a)=-2.
故选:A.
点评 本题考查函数值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若集合M={1,3},N={1,3,5},则满足M∪X=N的集合X的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.已知集合S=$\left\{{1,2,3}\right\},T=\left\{{x\left|{\frac{x-1}{x-3}≤0}\right.}\right\}$,则S∩T=( )
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
9.已知曲线C1:y=x2与曲线C2:$y=lnx(x>\frac{{\sqrt{2}}}{2})$,直线l是曲线C1和曲线C2的公切线,设直线l与曲线C1切点为P,则点P的横坐标t满足( )
| A. | $0<t<\frac{1}{2e}$ | B. | $\frac{1}{2e}<t<\frac{1}{2}$ | C. | $\frac{1}{2}<t<\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}<t<\sqrt{2}$ |
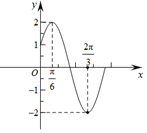 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.