题目内容
6.已知向量$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(-1,2),那么向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角余弦值是$\frac{\sqrt{10}}{10}$.分析 根据向量的夹角公式计算即可
解答 解:∵向量$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(-1,2),
∴|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=$\sqrt{5}$,$\overrightarrow{a}•\overrightarrow{b}$=1×(-1)+1×2=1,
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{1}{\sqrt{2}×\sqrt{5}}$=$\frac{\sqrt{10}}{10}$,
故答案为:$\frac{{\sqrt{10}}}{10}$
点评 本题考查了向量的夹角公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.复数$\frac{2}{i(3-i)}$=( )
| A. | $\frac{1-3i}{5}$ | B. | $\frac{1+3i}{5}$ | C. | $\frac{3+i}{5}$ | D. | $\frac{3-i}{5}$ |
14.若复数z满足i(z-1)=1+i(i虚数单位),则z=( )
| A. | 2-i | B. | 2+i | C. | 1-2i | D. | 1+2i |
11.已知:(logax)′=$\frac{1}{xlna}$,f′(x)是定义在(0,+∞)上的函数f(x)的导函数,若方程f′(x)=0无解,且对?x∈(0,+∞),f[f(x)-log2016x]=2017,设关于x的方程f(x)+f′(x)=t有解,则t的取值范围是( )
| A. | [2016+$\frac{1}{ln2016}$,+∞) | B. | (2016+$\frac{1}{ln2016}$,+∞) | C. | [2016-$\frac{1}{ln2016}$,+∞) | D. | (2016-$\frac{1}{ln2016}$,+∞) |
18.已知2sinx=1+cosx,则$cot\frac{x}{2}$=( )
| A. | 2 | B. | 2或$\frac{1}{2}$ | C. | 2或0 | D. | $\frac{1}{2}$或0 |
15.若集合M={1,3},N={1,3,5},则满足M∪X=N的集合X的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
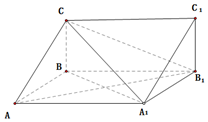 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.