题目内容
5.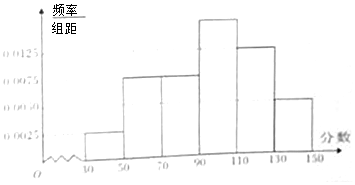 某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:(Ⅰ)求获得参赛资格的人数;
(Ⅱ)若大赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为$\frac{1}{9}$,求甲在初赛中答题个数X的分布列及数学期望E(X)
分析 (Ⅰ)由题意计算成绩在[90,110)之间的频率,求出获得参赛资格的人数;
(Ⅱ)求出甲答对每一个问题的概率p,得出甲在初赛中答题个数X的所有取值,
计算对应的概率值,写出X的分布列,计算数学期望值.
解答 解:(Ⅰ)由题意知,成绩在[90,110)之间的频率为
1-20×(0.0025+0.005+0.0075×2+0.0125)=0.3,
0.3+(0.0125+0.0050)×20=0.65,
故所求获得参赛资格的人数为800×0.65=520;
(Ⅱ)设甲答对每一个问题的概率为p,则(1-p)2=$\frac{1}{9}$,
∴p=$\frac{2}{3}$,
甲在初赛中答题个数X的所有取值为3,4,5;
则P(X=3)=${(\frac{2}{3})}^{3}$+${(\frac{1}{3})}^{3}$=$\frac{1}{3}$;
P(X=4)=${C}_{3}^{2}$•${(\frac{2}{3})}^{2}$•$\frac{1}{3}$•$\frac{2}{3}$+${C}_{3}^{2}$•${(\frac{1}{3})}^{2}$•$\frac{2}{3}$•$\frac{1}{3}$=$\frac{10}{27}$;
P(X=5)=${C}_{4}^{2}$•${(\frac{2}{3})}^{2}$${(\frac{1}{3})}^{2}$=$\frac{8}{27}$;
故X的分布列为:
| X | 3 | 4 | 5 |
| P | $\frac{1}{3}$ | $\frac{10}{27}$ | $\frac{8}{27}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的应用问题,是基础题.

练习册系列答案
相关题目
2.若抛物线y2=2px(p>0)的焦点与双曲线$\frac{{x}^{2}}{3}$-y2=1的一个焦点重合,则p=( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4 |
13.已知点P(4,-3)在角φ的终边上,函数f(x)=sin(ωx+φ)(ω>0)图象上与y轴最近的两个对称中心间的距离为$\frac{π}{2}$,则f($\frac{π}{8}$)的值为( )
| A. | $\frac{7\sqrt{2}}{10}$ | B. | -$\frac{7\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |
17.设实数a>b>0,c>0,则下列不等式一定正确的是( )
| A. | $0<\frac{a}{b}<1$ | B. | $ln\frac{a}{b}>0$ | C. | ca>cb | D. | ac-bc<0 |
15.已知集合$M=\{x|\frac{2}{x}<1\}$,$N=\{y|y=\sqrt{x-1}\}$,则(∁RM)∩N=( )
| A. | (0,2] | B. | [0,2] | C. | ∅ | D. | [1,2] |