题目内容
20.已知集合A={-1,0,1},B={x|x2<1},则A∩B=( )| A. | ∅ | B. | {0} | C. | {-1,1} | D. | {-1,0,1} |
分析 解不等式得集合B,根据交集的定义写出A∩B.
解答 解:集合A={-1,0,1},
B={x|x2<1}={x|-1<x<1},
则A∩B={0}.
故选:B.
点评 本题考查了解不等式与交集的运算问题,是基础题.

练习册系列答案
相关题目
8.已知集合S=$\left\{{1,2,3}\right\},T=\left\{{x\left|{\frac{x-1}{x-3}≤0}\right.}\right\}$,则S∩T=( )
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
15.已知集合$M=\{x|\frac{2}{x}<1\}$,$N=\{y|y=\sqrt{x-1}\}$,则(∁RM)∩N=( )
| A. | (0,2] | B. | [0,2] | C. | ∅ | D. | [1,2] |
9.已知曲线C1:y=x2与曲线C2:$y=lnx(x>\frac{{\sqrt{2}}}{2})$,直线l是曲线C1和曲线C2的公切线,设直线l与曲线C1切点为P,则点P的横坐标t满足( )
| A. | $0<t<\frac{1}{2e}$ | B. | $\frac{1}{2e}<t<\frac{1}{2}$ | C. | $\frac{1}{2}<t<\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}<t<\sqrt{2}$ |
10.设$(1+i)(x+yi)=2\sqrt{2}i$,其中x,y是实数,则|x+yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
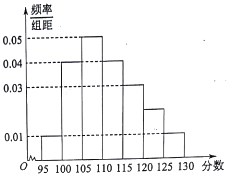 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.